In graph theory, ΔY- and YΔ-transformations (also written delta-wye and wye-delta) are a pair of operations on graphs. A ΔY-transformation replaces a triangle by a vertex of degree three; and conversely, a YΔ-transformation replaces a vertex of degree three by a triangle. The names for the operations derive from the shapes of the involved subgraphs, which look respectively like the letter Y and the Greek capital letter Δ.
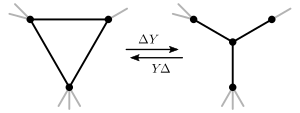
A YΔ-transformation may create parallel edges, even if applied to a simple graph. For this reason ΔY- and YΔ-transformations are most naturally considered as operations on multigraphs. On multigraphs both operations preserve the edge count and are exact inverses of each other. In the context of simple graphs it is common to combine a YΔ-transformation with a subsequent normalization step that reduces parallel edges to a single edge. This may no longer preserve the number of edges, nor be exactly reversible via a ΔY-transformation.

Formal definition
editLet be a graph (potentially a multigraph).
Suppose contains a triangle with vertices and edges . A ΔY-transformation of at deletes the edges and adds a new vertex adjacent to each of .
Conversely, if is a vertex of degree three with neighbors , then a YΔ-transformation of at deletes and adds three new edges , where connects and . If the resulting graph should be a simple graph, then any resulting parallel edges are to be replaced by a single edge.
Relevance
editΔY- and YΔ-transformations are a tool both in pure graph theory as well as applications.
Both operations preserve a number of natural topological properties of graphs. For example, applying a YΔ-transformation to a 3-vertex of a planar graph, or a ΔY-transformation to a triangular face of a planar graph, results again in a planar graph.[1] This was used in the original proof of Steinitz's theorem, showing that every 3-connected planar graph is the edge graph of a polyhedron. Applying ΔY- and YΔ-transformations to a linkless graph results again in a linkless graph.[2] This fact is used to compactly describe the forbidden minors of the associated graph classes as ΔY-families generated from a small number of graphs (see the section on ΔY-families below).
A particularly relevant application exists in electrical engineering in the study of three-phase power systems (see Y-Δ transform (electrical engineering)).[3] In this context they are also known as star-triangle transformations and are a special case of star-mesh transformations.
ΔY-families
editThe ΔY-family generated by a graph is the smallest family of graphs that contains and is closed under YΔ- and ΔY-transformations. Equivalently, it is constructed from by recursively applying these transformations until no new graph is generated. If is a finite graph it generates a finite ΔY-family, all members of which have the same edge count.
The ΔY-family generated by several graphs is the smallest family that contains all these graphs and is closed under YΔ- and ΔY-transformation.
Some notable families are generated in this way:
- the Petersen family is generated from the complete graph . It consists of the six forbidden minors for the class of linkless graphs.[2]
- the Heawood family is generated from and . It consists of 78 graphs, each of which is a forbidden minors for the class of 4-flat graphs.[4]
YΔY-reducible graphs
editA graph is YΔY-reducible if it can be reduced to a single vertex by a sequence of ΔY- or YΔ-transformations and the following normalization steps:
- removing a loop,
- removing a parallel edge,
- removing a vertex of degree one,
- smoothing out a vertex of degree two, i.e., replacing it by a single edge between its two former neighbors.
The YΔY-reducible graphs form a minor closed family and therefore have a forbidden minor characterization (by the Robertson–Seymour theorem). The graphs of the Petersen family constitute some (but not all) of the excluded minors.[5] In fact, already more than 68 billion excluded minor are known.[6]
The class of YΔY-reducible graphs lies between the classes of planar graphs and linkless graphs: each planar graph is YΔY-reducible, while each YΔY-reducible graph is linkless. Both inclusions are strict: is not planar but YΔY-reducible, while the graph in the figure is not YΔY-reducible but linkless.[5]
References
edit- ^ Truemper, K. (1989). On the delta‐wye reduction for planar graphs. Journal of graph theory, 13(2), 141–148.
- ^ a b Robertson, Neil; Seymour, P. D.; Thomas, Robin (1993), "Linkless embeddings of graphs in 3-space", Bulletin of the American Mathematical Society, 28 (1): 84–89, arXiv:math/9301216, doi:10.1090/S0273-0979-1993-00335-5, MR 1164063.
- ^ Johnson, D. E., Hilburn, J. L., Johnson, J. R., & Scott, P. D. (1986). Basic electric circuit analysis. Englewood Cliffs: Prentice-Hall.
- ^ van der Holst, H. (2006). Graphs and obstructions in four dimensions. Journal of Combinatorial Theory, Series B, 96(3), 388–404.
- ^ a b Truemper, Klaus (1992), Matroid Decomposition (PDF), Academic Press, pp. 100–101
- ^ Yu, Y. (2006). More forbidden minors for Wye-Delta-Wye reducibility. the electronic journal of combinatorics, R7-R7.