In mathematics, the extended real number system[a] is obtained from the real number system by adding two elements denoted and [b] that are respectively greater and lower than every real number. This allows for treating the potential infinities of infinitely increasing sequences and infinitely decreasing series as actual infinities. For example, the infinite sequence of the natural numbers increases infinitively and has no upper bound in the real number system (a potential infinity); in the extended real number line, the sequence has as its least upper bound and as its limit (an actual infinity). In calculus and mathematical analysis, the use of and as actual limits extends significantly the possible computations.[1] It is the Dedekind–MacNeille completion of the real numbers.
The extended real number system is denoted or or [2] When the meaning is clear from context, the symbol is often written simply as [2]
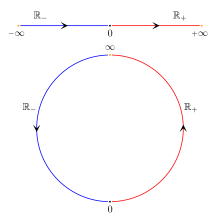
There is also a distinct projectively extended real line where and are not distinguished, i.e., there is a single actual infinity for both infinitely increasing sequences and infinitely decreasing sequences that is denoted as just or as .
Motivation
editLimits
editThe extended number line is often useful to describe the behavior of a function when either the argument or the function value gets "infinitely large" in some sense. For example, consider the function defined by
The graph of this function has a horizontal asymptote at Geometrically, when moving increasingly farther to the right along the -axis, the value of approaches 0. This limiting behavior is similar to the limit of a function in which the real number approaches except that there is no real number that approaches when increases infinitely. Adjoining the elements and to enables a definition of "limits at infinity" which is very similar to the usual defininion of limits, except that is replaced by (for ) or (for ). This allows proving and writing
Measure and integration
editThis section may be confusing or unclear to readers. In particular, since this is a subsection of section "Motivation", it must be understandable by readers who know nothing more than the basic definition of an integral. (September 2024) |
In measure theory, it is often useful to allow sets that have infinite measure and integrals whose value may be infinite.
Such measures arise naturally out of calculus. For example, in assigning a measure to that agrees with the usual length of intervals, this measure must be larger than any finite real number. Also, when considering improper integrals, such as
the value "infinity" arises. Finally, it is often useful to consider the limit of a sequence of functions, such as
Without allowing functions to take on infinite values, such essential results as the monotone convergence theorem and the dominated convergence theorem would not make sense.
Order and topological properties
editThe extended real number system , defined as or , can be turned into a totally ordered set by defining for all With this order topology, has the desirable property of compactness: Every subset of has a supremum and an infimum[3] (the infimum of the empty set is , and its supremum is ). Moreover, with this topology, is homeomorphic to the unit interval Thus the topology is metrizable, corresponding (for a given homeomorphism) to the ordinary metric on this interval. There is no metric, however, that is an extension of the ordinary metric on
In this topology, a set is a neighborhood of if and only if it contains a set for some real number The notion of the neighborhood of can be defined similarly. Using this characterization of extended-real neighborhoods, limits with tending to or , and limits "equal" to and , reduce to the general topological definition of limits—instead of having a special definition in the real number system.
Arithmetic operations
editThe arithmetic operations of can be partially extended to as follows:[2]
For exponentiation, see Exponentiation § Limits of powers. Here, means both and while means both and
The expressions and (called indeterminate forms) are usually left undefined. These rules are modeled on the laws for infinite limits. However, in the context of probability or measure theory, is often defined as [4]
When dealing with both positive and negative extended real numbers, the expression is usually left undefined, because, although it is true that for every real nonzero sequence that converges to the reciprocal sequence is eventually contained in every neighborhood of it is not true that the sequence must itself converge to either or Said another way, if a continuous function achieves a zero at a certain value then it need not be the case that tends to either or in the limit as tends to This is the case for the limits of the identity function when tends to and of (for the latter function, neither nor is a limit of even if only positive values of are considered).
However, in contexts where only non-negative values are considered, it is often convenient to define For example, when working with power series, the radius of convergence of a power series with coefficients is often defined as the reciprocal of the limit-supremum of the sequence . Thus, if one allows to take the value then one can use this formula regardless of whether the limit-supremum is or not.
Algebraic properties
editWith the arithmetic operations defined above, is not even a semigroup, let alone a group, a ring or a field as in the case of However, it has several convenient properties:
- and are either equal or both undefined.
- and are either equal or both undefined.
- and are either equal or both undefined.
- and are either equal or both undefined
- and are equal if both are defined.
- If and if both and are defined, then
- If and and if both and are defined, then
In general, all laws of arithmetic are valid in as long as all occurring expressions are defined.
Miscellaneous
editSeveral functions can be continuously extended to by taking limits. For instance, one may define the extremal points of the following functions as:
Some singularities may additionally be removed. For example, the function can be continuously extended to (under some definitions of continuity), by setting the value to for and for and On the other hand, the function cannot be continuously extended, because the function approaches as approaches from below, and as approaches from above, i.e., the function not converging to the same value as its independent variable approaching to the same domain element from both the positive and negative value sides.
A similar but different real-line system, the projectively extended real line, does not distinguish between and (i.e. infinity is unsigned).[5] As a result, a function may have limit on the projectively extended real line, while in the extended real number system only the absolute value of the function has a limit, e.g. in the case of the function at On the other hand, on the projectively extended real line, and correspond to only a limit from the right and one from the left, respectively, with the full limit only existing when the two are equal. Thus, the functions and cannot be made continuous at on the projectively extended real line.
See also
edit- Division by zero
- Extended complex plane
- Extended natural numbers
- Improper integral
- Infinity
- Log semiring
- Series (mathematics)
- Projectively extended real line
- Computer representations of extended real numbers, see Floating-point arithmetic § Infinities and IEEE floating point
Notes
edit- ^ Some authors use Affinely extended real number system and Affinely extended real number line, although the extended real numbers do not form an affine line.
- ^ Read as "positive infinity" and "negative infinity" respectively.
References
edit- ^ Wilkins, David (2007). "Section 6: The Extended Real Number System" (PDF). maths.tcd.ie. Retrieved 2019-12-03.
- ^ a b c Weisstein, Eric W. "Affinely Extended Real Numbers". mathworld.wolfram.com. Retrieved 2019-12-03.
- ^ Oden, J. Tinsley; Demkowicz, Leszek (16 January 2018). Applied Functional Analysis (3 ed.). Chapman and Hall/CRC. p. 74. ISBN 9781498761147. Retrieved 8 December 2019.
- ^ "extended real number in nLab". ncatlab.org. Retrieved 2019-12-03.
- ^ Weisstein, Eric W. "Projectively Extended Real Numbers". mathworld.wolfram.com. Retrieved 2019-12-03.
Further reading
edit- Aliprantis, Charalambos D.; Burkinshaw, Owen (1998), Principles of Real Analysis (3rd ed.), San Diego, CA: Academic Press, Inc., p. 29, ISBN 0-12-050257-7, MR 1669668
- David W. Cantrell. "Affinely Extended Real Numbers". MathWorld.





![{\displaystyle [-\infty ,+\infty ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a7a5a5ba47896e8fdd43cf7f311db27350f0f8ff)



