Boerdijk–Coxeter helix

Coxeter helices from regular tetrahedra

CCW and CW turning

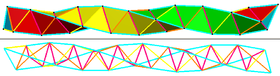Edges can be colored into 6 groups, 3 main helixes (cyan), with the concave edges forming a slow forward helix (magenta), and two backwards helixes (yellow and orange)

The Boerdijk–Coxeter helix, named after H. S. M. Coxeter and Arie Hendrick Boerdijk, is a linear stacking of regular tetrahedra, arranged so that the edges of the complex that belong to only one tetrahedron form three intertwined helices. There are two chiral forms, with either clockwise or counterclockwise windings. Unlike any other stacking of Platonic solids, the Boerdijk–Coxeter helix is not rotationally repetitive in 3-dimensional space. Even in an infinite string of stacked tetrahedra, no two tetrahedra will have the same orientation, because the helical pitch per cell is not a rational fraction of the circle. However, modified forms of this helix have been found which are rotationally repetitive, and in 4-dimensional space this helix repeats in rings of exactly 30 tetrahedral cells that tessellate the 3-sphere surface of the 600-cell, one of the six regular convex polychora.

A Boerdijk helical sphere packing has each sphere centered at a vertex of the Coxeter helix. Each sphere is in contact with 6 neighboring spheres.

Buckminster Fuller named it a tetrahelix and considered them with regular and irregular tetrahedral elements.

Geometry

The coordinates of vertices of Boerdijk–Coxeter helix composed of tetrahedrons with unit edge length can be written in the form

$(r\cos n\theta ,r\sin n\theta ,nh)$

where $r=3{\sqrt {3}}/10$, $\theta =\pm \cos ^{-1}(-2/3)\approx 131.81^{\circ }$, $h=1/{\sqrt {10}}$ and $n$ is an arbitrary integer. The two different values of $\theta$ correspond to two chiral forms. All vertices are located on the cylinder with radius $r$ along z-axis. Given how the tetrahedra alternate, this gives an apparent twist of $2\theta -{\frac {4}{3}}\pi \approx 23.62^{\circ }$ every two tetrahedra. There is another inscribed cylinder with radius $3{\sqrt {2}}/20$ inside the helix.

Higher-dimensional geometry

30 tetrahedral ring from 600-cell projection

The 600-cell partitions into 20 rings of 30 tetrahedra, each a Boerdijk–Coxeter helix. When superimposed onto the 3-sphere curvature it becomes periodic, with a period of ten vertices, encompassing all 30 cells. The collective of such helices in the 600-cell represent a discrete Hopf fibration. While in 3 dimensions the edges are helices, in the imposed 3-sphere topology they are geodesics and have no torsion. They spiral around each other naturally due to the Hopf fibration. The collective of edges forms another discrete Hopf fibration of 12 rings with 10 vertices each. These correspond to rings of 10 dodecahedrons in the dual 120-cell.

In addition, the 16-cell partitions into two 8-tetrahedron rings, four edges long, and the 5-cell partitions into a single degenerate 5-tetrahedron ring.

4-polytope	Rings	Tetrahedra/ring	Cycle lengths	Net	Projection
600-cell	20	30	30, 103, 152
16-cell	2	8	8, 8, 42
5-cell	1	5	(5, 5), 5

Related polyhedral helixes

Equilateral square pyramids can also be chained together as a helix, with two vertex configurations, 3.4.3.4 and 3.3.4.3.3.4. This helix exists as finite ring of 30 pyramids in a 4-dimensional polytope.

And equilateral pentagonal pyramids can be chained with 3 vertex configurations, 3.3.5, 3.5.3.5, and 3.3.3.5.3.3.5:

In architecture

The Art Tower Mito is based on a Boerdijk–Coxeter helix.

See also

• Clifford parallel cell rings
• Toroidal polyhedron
• Line group#Helical symmetry
• Skew apeirogon#Helical apeirogons in 3-dimensions

References

• Coxeter, H. S. M. (1974). Regular Complex Polytopes. Cambridge University Press. ISBN 052120125X.
• Boerdijk, A.H. (1952). "Some remarks concerning close-packing of equal spheres". Philips Res. Rep. 7: 303–313.
• Fuller, R.Buckminster (1975). Applewhite, E.J. (ed.). Synergetics. Macmillan.
• Pugh, Anthony (1976). "5. Joining polyhedra §5.36 Tetrahelix". Polyhedra: A visual approach. University of California Press. p. 53. ISBN 978-0-520-03056-5.
• Sadler, Garrett; Fang, Fang; Kovacs, Julio; Klee, Irwin (2013). "Periodic modification of the Boerdijk-Coxeter helix (tetrahelix)". arXiv:1302.1174v1 [math.MG].
• Lord, E.A.; Ranganathan, S. (2004). "The γ-brass structure and the Boerdijk–Coxeter helix" (PDF). Journal of Non-Crystalline Solids. 334–335: 123–5. Bibcode:2004JNCS..334..121L. doi:10.1016/j.jnoncrysol.2003.11.069.
• Zhu, Yihan; He, Jiating; Shang, Cheng; Miao, Xiaohe; Huang, Jianfeng; Liu, Zhipan; Chen, Hongyu; Han, Yu (2014). "Chiral Gold Nanowires with Boerdijk–Coxeter–Bernal Structure". J. Am. Chem. Soc. 136 (36): 12746–52. doi:10.1021/ja506554j. PMID 25126894.
• Lord, Eric A.; Mackay, Alan L.; Ranganathan, S. (2006). "§4.5 The Boerdijk–Coxeter helix". New Geometries for New Materials. Cambridge University Press. p. 64. ISBN 978-0-521-86104-5.
• Banchoff, Thomas F. (1988). "Geometry of the Hopf Mapping and Pinkall's Tori of Given Conformal Type". In Tangora, Martin (ed.). Computers in Algebra. New York and Basel: Marcel Dekker. pp. 57–62.
• Banchoff, Thomas F. (2013). "Torus Decompostions of Regular Polytopes in 4-space". In Senechal, Marjorie (ed.). Shaping Space. Springer New York. pp. 257–266. doi:10.1007/978-0-387-92714-5_20. ISBN 978-0-387-92713-8.
• Sadoc, J.F.; Rivier, N. (1999). "Boerdijk-Coxeter helix and biological helices". The European Physical Journal B. 12 (2): 309–318. Bibcode:1999EPJB...12..309S. doi:10.1007/s100510051009. S2CID 92684626.
• Sadoc, Jean-Francois (2001). "Helices and helix packings derived from the {3,3,5} polytope". European Physical Journal E. 5: 575–582. doi:10.1007/s101890170040. S2CID 121229939.

External links

• Boerdijk-Coxeter helix animation
• Tetrahelix Data