Dark matter halo

"Dark halo" redirects here. Not to be confused with the hacker group Dark Halo, also known as Cozy Bear.

In modern models of physical cosmology, a dark matter halo is a basic unit of cosmological structure. It is a hypothetical region that has decoupled from cosmic expansion and contains gravitationally bound matter. A single dark matter halo may contain multiple virialized clumps of dark matter bound together by gravity, known as subhalos. Modern cosmological models, such as ΛCDM, propose that dark matter halos and subhalos may contain galaxies. The dark matter halo of a galaxy envelops the galactic disc and extends well beyond the edge of the visible galaxy. Thought to consist of dark matter, halos have not been observed directly. Their existence is inferred through observations of their effects on the motions of stars and gas in galaxies and gravitational lensing. Dark matter halos play a key role in current models of galaxy formation and evolution. Theories that attempt to explain the nature of dark matter halos with varying degrees of success include cold dark matter (CDM), warm dark matter, and massive compact halo objects (MACHOs).

Simulated dark matter halo from a cosmological N-body simulation

Galaxy rotation curve for the Milky Way. Vertical axis is speed of rotation about the galactic center. Horizontal axis is distance from the galactic center. The sun is marked with a yellow ball. The observed curve of speed of rotation is blue. The predicted curve based upon stellar mass and gas in the Milky Way is red. Scatter in observations roughly indicated by gray bars. The difference is due to dark matter or perhaps a modification of the law of gravity.

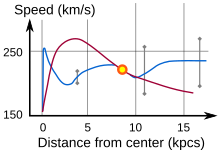
Rotation curves as evidence of a dark matter halo

The presence of dark matter (DM) in the halo is inferred from its gravitational effect on a spiral galaxy's rotation curve. Without large amounts of mass throughout the (roughly spherical) halo, the rotational velocity of the galaxy would decrease at large distances from the galactic center, just as the orbital speeds of the outer planets decrease with distance from the Sun. However, observations of spiral galaxies, particularly radio observations of line emission from neutral atomic hydrogen (known, in astronomical parlance, as 21 cm Hydrogen line, H one, and H I line), show that the rotation curve of most spiral galaxies flattens out, meaning that rotational velocities do not decrease with distance from the galactic center. The absence of any visible matter to account for these observations implies either that unobserved (dark) matter, first proposed by Ken Freeman in 1970, exist, or that the theory of motion under gravity (general relativity) is incomplete. Freeman noticed that the expected decline in velocity was not present in NGC 300 nor M33, and considered an undetected mass to explain it. The DM Hypothesis has been reinforced by several studies.

Formation and structure of dark matter halos

The formation of dark matter halos is believed to have played a major role in the early formation of galaxies. During initial galactic formation, the temperature of the baryonic matter should have still been much too high for it to form gravitationally self-bound objects, thus requiring the prior formation of dark matter structure to add additional gravitational interactions. The current hypothesis for this is based on cold dark matter (CDM) and its formation into structure early in the universe.

The hypothesis for CDM structure formation begins with density perturbations in the Universe that grow linearly until they reach a critical density, after which they would stop expanding and collapse to form gravitationally bound dark matter halos. The spherical collapse framework analytically models the formation and growth of such halos. These halos would continue to grow in mass (and size), either through accretion of material from their immediate neighborhood, or by merging with other halos. Numerical simulations of CDM structure formation have been found to proceed as follows: A small volume with small perturbations initially expands with the expansion of the Universe. As time proceeds, small-scale perturbations grow and collapse to form small halos. At a later stage, these small halos merge to form a single virialized dark matter halo with an ellipsoidal shape, which reveals some substructure in the form of dark matter sub-halos.

The use of CDM overcomes issues associated with the normal baryonic matter because it removes most of the thermal and radiative pressures that were preventing the collapse of the baryonic matter. The fact that the dark matter is cold compared to the baryonic matter allows the DM to form these initial, gravitationally bound clumps. Once these subhalos formed, their gravitational interaction with baryonic matter is enough to overcome the thermal energy, and allow it to collapse into the first stars and galaxies. Simulations of this early galaxy formation matches the structure observed by galactic surveys as well as observation of the Cosmic Microwave Background.

Density profiles

A commonly used model for galactic dark matter halos is the pseudo-isothermal halo:

$\rho (r)=\rho _{o}\left[1+\left({\frac {r}{r_{c}}}\right)^{2}\right]^{-1}$

where $\rho _{o}$ denotes the finite central density and $r_{c}$ the core radius. This provides a good fit to most rotation curve data. However, it cannot be a complete description, as the enclosed mass fails to converge to a finite value as the radius tends to infinity. The isothermal model is, at best, an approximation. Many effects may cause deviations from the profile predicted by this simple model. For example, (i) collapse may never reach an equilibrium state in the outer region of a dark matter halo, (ii) non-radial motion may be important, and (iii) mergers associated with the (hierarchical) formation of a halo may render the spherical-collapse model invalid.

Numerical simulations of structure formation in an expanding universe lead to the empirical NFW (Navarro–Frenk–White) profile:

$\rho (r)={\frac {\rho _{crit}\delta _{c}}{\left({\frac {r}{r_{s}}}\right)\left(1+{\frac {r}{r_{s}}}\right)^{2}}}$

where $r_{s}$ is a scale radius, $\delta _{c}$ is a characteristic (dimensionless) density, and $\rho _{crit}$ = $3H^{2}/8\pi G$ is the critical density for closure. The NFW profile is called 'universal' because it works for a large variety of halo masses, spanning four orders of magnitude, from individual galaxies to the halos of galaxy clusters. This profile has a finite gravitational potential even though the integrated mass still diverges logarithmically. It has become conventional to refer to the mass of a halo at a fiducial point that encloses an overdensity 200 times greater than the critical density of the universe, though mathematically the profile extends beyond this notational point. It was later deduced that the density profile depends on the environment, with the NFW appropriate only for isolated halos. NFW halos generally provide a worse description of galaxy data than does the pseudo-isothermal profile, leading to the cuspy halo problem.

Higher resolution computer simulations are better described by the Einasto profile:

$\rho (r)=\rho _{e}\exp \left[-d_{n}\left(\left({\frac {r}{r_{e}}}\right)^{\frac {1}{n}}-1\right)\right]$

where r is the spatial (i.e., not projected) radius. The term $d_{n}$ is a function of n such that $\rho _{e}$ is the density at the radius $r_{e}$ that defines a volume containing half of the total mass. While the addition of a third parameter provides a slightly improved description of the results from numerical simulations, it is not observationally distinguishable from the 2 parameter NFW halo, and does nothing to alleviate the cuspy halo problem.

Shape

The collapse of overdensities in the cosmic density field is generally aspherical. So, there is no reason to expect the resulting halos to be spherical. Even the earliest simulations of structure formation in a CDM universe emphasized that the halos are substantially flattened. Subsequent work has shown that halo equidensity surfaces can be described by ellipsoids characterized by the lengths of their axes.

Because of uncertainties in both the data and the model predictions, it is still unclear whether the halo shapes inferred from observations are consistent with the predictions of ΛCDM cosmology.

Halo substructure

Up until the end of the 1990s, numerical simulations of halo formation revealed little substructure. With increasing computing power and better algorithms, it became possible to use greater numbers of particles and obtain better resolution. Substantial amounts of substructure are now expected. When a small halo merges with a significantly larger halo it becomes a subhalo orbiting within the potential well of its host. As it orbits, it is subjected to strong tidal forces from the host, which cause it to lose mass. In addition the orbit itself evolves as the subhalo is subjected to dynamical friction which causes it to lose energy and angular momentum to the dark matter particles of its host. Whether a subhalo survives as a self-bound entity depends on its mass, density profile, and its orbit.

Angular momentum

As originally pointed out by Hoyle and first demonstrated using numerical simulations by Efstathiou & Jones, asymmetric collapse in an expanding universe produces objects with significant angular momentum.

Numerical simulations have shown that the spin parameter distribution for halos formed by dissipation-less hierarchical clustering is well fit by a log-normal distribution, the median and width of which depend only weakly on halo mass, redshift, and cosmology:

$\rho (\lambda )d\lambda ={\frac {1}{{\sqrt {2\pi }}\sigma _{ln\lambda }}}\exp \left[-{\frac {\ln \left({\frac {\lambda }{\bar {\lambda }}}\right)^{2}}{2\sigma _{\ln \lambda }^{2}}}\right]{\frac {d\lambda }{\lambda }}$

with ${\bar {\lambda }}\approx 0.035$ and $\sigma _{ln\lambda }\approx 0.5$. At all halo masses, there is a marked tendency for halos with higher spin to be in denser regions and thus to be more strongly clustered.

Milky Way dark matter halo

The visible disk of the Milky Way Galaxy is thought to be embedded in a much larger, roughly spherical halo of dark matter. The dark matter density drops off with distance from the galactic center. It is now believed that about 95% of the galaxy is composed of dark matter, a type of matter that does not seem to interact with the rest of the galaxy's matter and energy in any way except through gravity. The luminous matter makes up approximately 9×10¹⁰ solar masses. The dark matter halo is likely to include around 6×10¹¹ to 3×10¹² solar masses of dark matter. A 2014 Jeans analysis of stellar motions calculated the dark matter density (at the sun's distance from the galactic centre) = 0.0088 (+0.0024 −0.0018) solar masses/parsec^3.

See also

• Galaxy formation and evolution
• Galactic coordinate system – Celestial coordinate system in spherical coordinates, with the Sun as its center
• Galactic disc – Component of disc galaxies comprising gas and stars
• Bulge (astronomy) – Tightly packed group of stars within a larger formationPages displaying short descriptions of redirect targets
• Galactic halo – Spherical component of a galaxy which extends beyond the main, visible component
• Spiral arm – Spiral-shaped regions of enhanced brightness within the galactic disc in spiral galaxies
• Dark matter – Concept in cosmology
• Dark galaxy – A hypothesized galaxy with no, or very few, stars
• Press–Schechter formalism – A mathematical model used to predict the number of dark matter halos of a certain mass.

Further reading

• Bertone, Gianfranco (2010). Particle Dark Matter: Observations, Models and Searches. Cambridge University Press. p. 762. Bibcode:2010pdmo.book.....B. ISBN 978-0-521-76368-4. {{cite book}}: |journal= ignored (help)
• Wechsler, Risa H.; Tinker, Jeremy L. (14 September 2018). "The Connection Between Galaxies and Their Dark Matter Halos". Annual Review of Astronomy and Astrophysics. 56 (1): 435–487. arXiv:1804.03097. Bibcode:2018ARA&A..56..435W. doi:10.1146/annurev-astro-081817-051756. S2CID 119072496.

External links

• Rare Blob Unveiled: Evidence For Hydrogen Gas Falling Onto A Dark Matter Clump? European Southern Observatory (ScienceDaily) July 3, 2006
• Dark Matter Search Experiment , PICASSO Experiment
• Black Holes and Dark matter