Wikipedia

Teapot effect

(Redirected from Drip-catcher)

The teapot effect, also known as dribbling, is a fluid dynamics phenomenon that occurs when a liquid being poured from a container runs down the spout or the body of the vessel instead of flowing out in an arc.[1]

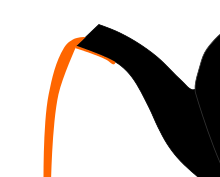
Diagram of tea running down the spout of a teapot

Markus Reiner coined the term "teapot effect" in 1956 to describe the tendency of liquid to dribble down the side of a vessel while pouring.[2][3] Reiner received his PhD at TU Wien in 1913 and made significant contributions to the development of the study of flow behavior known as rheology.[1] Reiner believed the teapot effect could be explained by Bernoulli's principle, which states that an increase in the speed of a fluid is always accompanied by a decrease in its pressure. When tea is poured from a teapot, the liquid's speed increases as it flows through the narrowing spout. This decrease in pressure was what Reiner thought to cause the liquid to dribble down the side of the pot.[4][3] However, a 2021 study found the primary cause of the phenomenon to be an interaction of inertia and capillary forces.[3] The study found that the smaller the angle between the container wall and the liquid surface, the more the teapot effect is slowed down.[5]

Research

edit

Around 1950, researchers from the Technion Institute in Haifa (Israel) and from New York University tried to explain this effect scientifically.[6] In fact, there are two phenomena that contribute to this effect: on the one hand, the Bernoulli equation is used to explain it, on the other hand, the adhesion between the liquid and the spout material is also important.

According to the Bernoulli explanation, the liquid is pressed against the inner edge of the spout when pouring out, because the pressure conditions at the end, the edge, change significantly; the surrounding air pressure pushes the liquid towards the spout. With the help of a suitable pot geometry (or a sufficiently high pouring speed) it can be avoided that the liquid reaches the spout and thus triggers the teapot effect. Laws of hydrodynamics (flow theory) describe this situation, the relevant ones are explained in the following sections.

Since adhesion also plays a role, the material of the spout or the type of liquid (water, alcohol or oil, for example) is also relevant for the occurrence of the teapot effect.

The Coandă effect is sometimes mentioned in this context,[7][8][9][10] but it is rarely cited in the scientific literature[8] and is therefore not precisely defined. Often several different phenomena seem to be mixed up in this one.

Continuity equation

edit

In hydrodynamics, the behavior of flowing liquids is illustrated by flow lines. They run in the same direction as the flow itself. If the outflowing liquid hits an edge, the flow is compressed into a smaller cross-section. It only does not break off if the flow rate of liquid particles remains constant, regardless of where an imaginary cross section (perpendicular to the flow) is located. So the same amount of mass must flow in through one cross-sectional area as flows out of another. One can now conclude from this, but also observe in reality, that the flow accelerates at bottlenecks and the streamlines are bundled. This situation describes the continuity equation for non-turbulent flows.

Bernoulli equation

edit

But what happens to the pressure conditions in the flow if you change the flow speed? The scientist Daniel Bernoulli dealt with this question as early as the beginning of the 18th century. Based on the considerations of continuity mentioned above, and incorporating the conservation of energy, he linked the two quantities of pressure and speed. The core statement of the Bernoulli equation is that the pressure in a liquid falls where the velocity increases (and vice versa): Flow according to Bernoulli and Venturi.

Impact

edit

The pressure in the flow is reduced at the edge of the can spout. However, since the air pressure on the outside of the flow is the same everywhere, there is a pressure difference that pushes the liquid to the edge. Depending on the materials used, the outside of the spout is now wetted during the flow process. At this point, additional interfacial forces occur : the liquid runs as a narrow trickle along the spout and can until it detaches from the underside.

The unwanted teapot effect only occurs when pouring slowly and carefully.[6] In fast pouring, the liquid flows out of the spout in an arc without dripping, so it is given a relatively high velocity with which the liquid moves away from the edge (see Torricelli outflow velocity). The pressure difference resulting from the Bernoulli equation is then not sufficient to influence the flow to such an extent that the liquid is pushed around the edge of the spout.

Since the flow conditions can be described mathematically, a critical outflow velocity is also defined. If it falls below when pouring, the liquid flows down the pot; it drips. Theoretically, this speed could be precisely calculated for a specific can geometry, the current air pressure and the fill level of the can, the spout material, the viscosity of the liquid and the pouring angle. Since, apart from the fill level, most of the influencing variables cannot be changed (at least not sufficiently precisely in practice), the only way to avoid the teapot effect is usually to choose a suitable geometry for the pot.

Another phenomenon is the reduction in air pressure between the spout and the jet of liquid due to the entrainment of gas molecules (one-sided water jet pumping effect), so that the air pressure on the opposite side would push the jet of liquid to the spout side. However, under the conditions usually prevailing when pouring tea, this effect will hardly appear.

Consequence

edit
 
Pot examples

A good jug should, regardless of fashion, have a spout with a tear-off edge (i.e. no rounded edge) to make it more difficult to run around the edge. More importantly, the spout should first lead upwards (regardless of the position in which the jug is held). As a result, the liquid would be forced to flow upwards after going around the edge of the spout when pouring, but this is prevented by gravity. The flow can thus resist wetting even when pouring slowly and the liquid does not reach the downwardly inclined part of the spout and the body of the jug.

The image on the right[clarification needed] shows three vessels with poor pouring behavior. Even in a horizontal position, that is standing on the table, the bottom edges of the spouts do not point upwards.[6] Behind are four vessels with good flow characteristics resulting from well formed tips. Here, the liquid rises at the lower edge of the spout at an angle of less than 45°.[6] In part, this only becomes apparent when one considers the normal maximum fill level: the glass carafe on the far right, for example, appears at first glance to be a poor pourer because of its slender neck. However, since such vessels are generally filled at most up to the edge of the round part of the flask, an advantageous rise at the neck is then obtained when pouring horizontally.Upward angle for the liquid when pouring. With the two lower jugs on the right, the high position of the spout (above the maximum filling level) means that the vessel has to be tilted quite a bit before pouring, so that the spout can also be pushed up directly after the edge (against gravity). indicates.

To avoid the teapot effect, the pot can be filled less, so that a larger tilting angle is necessary from the start. However, the effect or the ideal filling level again depends on the can geometry.

The teapot effect does not occur with bottles because the slender neck of the bottle always points upwards when pouring; the current would therefore have to "flow uphill" a long way.[6] Bottle-like containers are therefore often used for liquid chemicals in the laboratory. Certain materials are also used there to prevent dripping, for example glass, which can be easily shaped or even ground to create the sharpest possible edges, or Teflon, for example, which reduces the adhesion effect described above.

Drip catcher

edit

See also

edit

References

edit
  1. ^ a b "Why Teapots Always Drip – Scientists Finally Explain the "Teapot Effect"". SciTechDaily. Vienna University of Technology. 2022-01-09. Archived from the original on 2023-01-28. Retrieved 2022-07-02.
  2. ^ Reiner, Markus (September 1956). "The teapot effect...a problem". Physics Today. 9 (9). American Institute of Physics: 16. doi:10.1063/1.3060089. Retrieved 2023-01-28. (1 page)
  3. ^ a b c Ouellette, Jennifer (2021-11-10). "Dribble, dribble, dribble — Physicists say they've finally solved the teapot effect—for real this time - Is due to interplay of inertial viscous capillary forces—but gravity's less relevant". Ars Technica. Archived from the original on 2023-01-28. Retrieved 2022-07-02.
  4. ^ Keller, Joseph Bishop (1957). "Teapot Effect" (PDF). Journal of Applied Physics. 28 (8): 859–864. Bibcode:1957JAP....28..859K. doi:10.1063/1.1722875. Archived (PDF) from the original on 2022-03-13. Retrieved 2023-01-28. [1] (6 pages)
  5. ^ Scheichl, Bernhard; Bowles, Robert I.; Pasias, Georgios (2021-11-10) [2021-09-08, 2021-07-01, 2021-05-17, 2020-11-09]. "Developed liquid film passing a smoothed and wedge-shaped trailing edge: small-scale analysis and the 'teapot effect' at large Reynolds numbers". Journal of Fluid Mechanics. 926. Cambridge University Press: A25-1–A25-40, S1–S12. arXiv:2011.12168. Bibcode:2021JFM...926A..25S. doi:10.1017/jfm.2021.612. ISSN 0022-1120. S2CID 235444365. Archived from the original on 2023-01-28. Retrieved 2023-01-28. [2] (40+12 pages)
  6. ^ a b c d e Dittmar-Ilgen, Hannelore (2007) [2006, 2004]. "Immer Ärger mit tröpfelnden Kannen". Wie der Kork-Krümel ans Weinglas kommt - Physik für Genießer und Entdecker (in German) (1 ed.). Stuttgart, Germany: S. Hirzel Verlag [de]. pp. 21–25. ISBN 978-3-7776-1440-3. ISBN 978-3-7776-1440-3. (172+4 pages)
  7. ^ Reba, Imants (June 1966). "Applications of the Coanda Effect". Scientific American. Vol. 214, no. 6. pp. 84–92. Bibcode:1966SciAm.214f..84R. doi:10.1038/scientificamerican0666-84. JSTOR 24930967. Retrieved 2023-01-28. (9 pages)
  8. ^ a b Reiner, Markus (May 1967). "Teapot means Coanda". Letters. Physics Today. 20 (5). American Institute of Physics: 15. Bibcode:1967PhT....20e..15R. doi:10.1063/1.3034300. Retrieved 2023-01-28. (1 page)
  9. ^ Reiner, Markus (1969). Deformation, Strain and Flow - An Elementary Introduction To Rheology (3 ed.). H. K. Lewis & Co. Ltd. ISBN 0-71860162-9. (347 pages)
  10. ^ Ziegler, Alfred; Wodzinski, Ruth (2001) [2000, 1999]. "Die Physik des Fliegens als Bestandteil eines Unterrichts zur Strömungslehre: Zielsetzungen und Begründungen". Vorträge / Physikertagung, Deutsche Physikalische Gesellschaft, Fachausschuss Didaktik der Physik (Book, CD) (in German). Arbeitsgruppe Didaktik der Physik, Universität Kassel. pp. 549–552. Archived from the original on 2023-01-29. Retrieved 2023-01-29. Coanda-Effekt (bzw. "Kaffeekanneneffekt"-ein Tropfen folgt der Oberfläche) (NB. Calls the effect "coffeepot effect" rather than "teapot effect".)

Further reading

edit
Retrieved from "https://en.wikipedia.org/w/index.php?title=Teapot_effect&oldid=1260189946#Drip_catcher"