No higher resolution available.
Attractors-Orbit.gif (360 × 357 pixels, file size: 657 KB, MIME type: image/gif, looped, 91 frames, 9.1 s)
 | This is a file from the Wikimedia Commons. Information from its description page there is shown below. Commons is a freely licensed media file repository. You can help. |
Summary
| Description |
English: Visualization of how a number of randomly chosen initial conditions are all attracted to a stable orbit for the f-2(1-f²)f'+f=0 differential equation (i.e. the Van Der Pol oscillator). |
| Date | |
| Source | https://twitter.com/j_bertolotti/status/1450378380193538049 |
| Author | Jacopo Bertolotti |
| Permission (Reusing this file) |
https://twitter.com/j_bertolotti/status/1030470604418428929 |
Mathematica 12.0 code
points1 = RandomReal[{-4, 4}, {100, 2}];
dim = Dimensions[points1][[1]];
psol1 = ParametricNDSolveValue[{x''[t] - 2 (1 - x[t]^2) x'[t] + x[t] == 0,
x[0] == x0, x'[0] == v0}, {x}, {t, 0, 50}, {x0, v0}]
frames1 = Table[
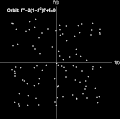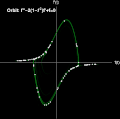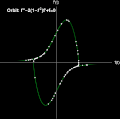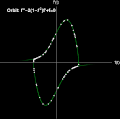
ParametricPlot[ Table[{psol1[points1[[j, 1]], points1[[j, 2]] ][[1]][t], psol1[points1[[j, 1]], points1[[j, 2]]][[1]]'[t]}, {j, 1, dim}], {t, 0, \[Tau]}, ColorFunction -> Function[{x, y, t}, Directive[ColorData["AvocadoColors"][t/\[Pi]] , Opacity[t^3] ] ], Background -> Black, PlotRange -> {{-5, 5}, {-5, 5}}, AspectRatio -> 1, Axes -> True, LabelStyle -> {White, FontSize -> 12}, AxesStyle -> White, Ticks -> None, AxesLabel -> {"f(t)", "f'(t)"}, Epilog -> {White, Style[Text["Orbit: f''-2(1-\!\(\*SuperscriptBox[\(f\), \(2\)]\))f'+f=0", {-2.2, 4.7}], Bold, FontSize -> 14], PointSize[0.01], Point[Table[{psol1[points1[[j, 1]], points1[[j, 2]] ][[1]][\[Tau]], psol1[points1[[j, 1]], points1[[j, 2]]][[1]]'[\[Tau]]}, {j, 1,dim}]]
}
]
, {\[Tau], 10^-3, 7, 7/50}];
ListAnimate[Join[Table[frames1[[1]], {5}], frames1]]
Licensing
I, the copyright holder of this work, hereby publish it under the following license:
 
|
This file is made available under the Creative Commons CC0 1.0 Universal Public Domain Dedication. |
| The person who associated a work with this deed has dedicated the work to the public domain by waiving all of their rights to the work worldwide under copyright law, including all related and neighboring rights, to the extent allowed by law. You can copy, modify, distribute and perform the work, even for commercial purposes, all without asking permission.
|
File history
Click on a date/time to view the file as it appeared at that time.
| Date/Time | Thumbnail | Dimensions | User | Comment | |
|---|---|---|---|---|---|
| current | 08:32, 19 October 2021 | | 360 × 357 (657 KB) | Berto | Uploaded own work with UploadWizard |
File usage
The following page uses this file:
