In computer science and graph theory, Karger's algorithm is a randomized algorithm to compute a minimum cut of a connected graph. It was invented by David Karger and first published in 1993.[1]
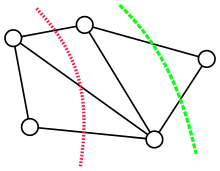
The idea of the algorithm is based on the concept of contraction of an edge in an undirected graph . Informally speaking, the contraction of an edge merges the nodes and into one, reducing the total number of nodes of the graph by one. All other edges connecting either or are "reattached" to the merged node, effectively producing a multigraph. Karger's basic algorithm iteratively contracts randomly chosen edges until only two nodes remain; those nodes represent a cut in the original graph. By iterating this basic algorithm a sufficient number of times, a minimum cut can be found with high probability.
The global minimum cut problem
editA cut in an undirected graph is a partition of the vertices into two non-empty, disjoint sets . The cutset of a cut consists of the edges between the two parts. The size (or weight) of a cut in an unweighted graph is the cardinality of the cutset, i.e., the number of edges between the two parts,
There are ways of choosing for each vertex whether it belongs to or to , but two of these choices make or empty and do not give rise to cuts. Among the remaining choices, swapping the roles of and does not change the cut, so each cut is counted twice; therefore, there are distinct cuts. The minimum cut problem is to find a cut of smallest size among these cuts.
For weighted graphs with positive edge weights the weight of the cut is the sum of the weights of edges between vertices in each part
which agrees with the unweighted definition for .
A cut is sometimes called a “global cut” to distinguish it from an “ - cut” for a given pair of vertices, which has the additional requirement that and . Every global cut is an - cut for some . Thus, the minimum cut problem can be solved in polynomial time by iterating over all choices of and solving the resulting minimum - cut problem using the max-flow min-cut theorem and a polynomial time algorithm for maximum flow, such as the push-relabel algorithm, though this approach is not optimal. Better deterministic algorithms for the global minimum cut problem include the Stoer–Wagner algorithm, which has a running time of .[2]
Contraction algorithm
editThe fundamental operation of Karger’s algorithm is a form of edge contraction. The result of contracting the edge is a new node . Every edge or for to the endpoints of the contracted edge is replaced by an edge to the new node. Finally, the contracted nodes and with all their incident edges are removed. In particular, the resulting graph contains no self-loops. The result of contracting edge is denoted .
The contraction algorithm repeatedly contracts random edges in the graph, until only two nodes remain, at which point there is only a single cut.
The key idea of the algorithm is that it is far more likely for non min-cut edges than min-cut edges to be randomly selected and lost to contraction, since min-cut edges are usually vastly outnumbered by non min-cut edges. Subsequently, it is plausible that the min-cut edges will survive all the edge contraction, and the algorithm will correctly identify the min-cut edge.
procedure contract( ): while choose uniformly at random return the only cut in
When the graph is represented using adjacency lists or an adjacency matrix, a single edge contraction operation can be implemented with a linear number of updates to the data structure, for a total running time of . Alternatively, the procedure can be viewed as an execution of Kruskal’s algorithm for constructing the minimum spanning tree in a graph where the edges have weights according to a random permutation . Removing the heaviest edge of this tree results in two components that describe a cut. In this way, the contraction procedure can be implemented like Kruskal’s algorithm in time .
The best known implementations use time and space, or time and space, respectively.[1]
Success probability of the contraction algorithm
editIn a graph with vertices, the contraction algorithm returns a minimum cut with polynomially small probability . Recall that every graph has cuts (by the discussion in the previous section), among which at most can be minimum cuts. Therefore, the success probability for this algorithm is much better than the probability for picking a cut at random, which is at most .
For instance, the cycle graph on vertices has exactly minimum cuts, given by every choice of 2 edges. The contraction procedure finds each of these with equal probability.
To further establish the lower bound on the success probability, let denote the edges of a specific minimum cut of size . The contraction algorithm returns if none of the random edges deleted by the algorithm belongs to the cutset . In particular, the first edge contraction avoids , which happens with probability . The minimum degree of is at least (otherwise a minimum degree vertex would induce a smaller cut where one of the two partitions contains only the minimum degree vertex), so . Thus, the probability that the contraction algorithm picks an edge from is
The probability that the contraction algorithm on an -vertex graph avoids satisfies the recurrence , with , which can be expanded as
Repeating the contraction algorithm
editBy repeating the contraction algorithm times with independent random choices and returning the smallest cut, the probability of not finding a minimum cut is
The total running time for repetitions for a graph with vertices and edges is .
Karger–Stein algorithm
editAn extension of Karger’s algorithm due to David Karger and Clifford Stein achieves an order of magnitude improvement.[3]
The basic idea is to perform the contraction procedure until the graph reaches vertices.
procedure contract( , ): while choose uniformly at random return
The probability that this contraction procedure avoids a specific cut in an -vertex graph is
This expression is approximately and becomes less than around . In particular, the probability that an edge from is contracted grows towards the end. This motivates the idea of switching to a slower algorithm after a certain number of contraction steps.
procedure fastmincut( ): if : return contract( , ) else: contract( , ) contract( , ) return min{fastmincut( ), fastmincut( )}
Analysis
editThe contraction parameter is chosen so that each call to contract has probability at least 1/2 of success (that is, of avoiding the contraction of an edge from a specific cutset ). This allows the successful part of the recursion tree to be modeled as a random binary tree generated by a critical Galton–Watson process, and to be analyzed accordingly.[3]
The probability that this random tree of successful calls contains a long-enough path to reach the base of the recursion and find is given by the recurrence relation
with solution . The running time of fastmincut satisfies
with solution . To achieve error probability , the algorithm can be repeated times, for an overall running time of . This is an order of magnitude improvement over Karger’s original algorithm.[3]
Improvement bound
editTo determine a min-cut, one has to touch every edge in the graph at least once, which is time in a dense graph. The Karger–Stein's min-cut algorithm takes the running time of , which is very close to that.
References
edit- ^ a b Karger, David (1993). "Global Min-cuts in RNC and Other Ramifications of a Simple Mincut Algorithm". Proc. 4th Annual ACM-SIAM Symposium on Discrete Algorithms.
- ^ Stoer, M.; Wagner, F. (1997). "A simple min-cut algorithm". Journal of the ACM. 44 (4): 585. doi:10.1145/263867.263872. S2CID 15220291.
- ^ a b c Karger, David R.; Stein, Clifford (1996). "A new approach to the minimum cut problem" (PDF). Journal of the ACM. 43 (4): 601. doi:10.1145/234533.234534. S2CID 5385337.



