Gyrobifastigium

Gyrobifastigium
Gyrobifastigium
Type	Johnson; J25 – J26 – J27
Faces	4 triangles; 4 squares
Edges	14
Vertices	8
Vertex configuration	4(3.42); 4(3.4.3.4)
Symmetry group	D2d
Properties	convex, honeycomb
Net

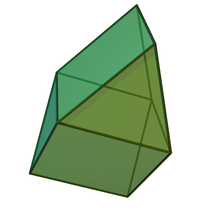
In geometry, the gyrobifastigium is a polyhedron that is constructed by attaching a triangular prism to square face of another one. It is an example of a Johnson solid. It is the only Johnson solid that can tile three-dimensional space.^[1]^[2]

Construction and its naming

The gyrobifastigium can be constructed by attaching two triangular prisms along corresponding square faces, giving a quarter-turn to one prism.^[3] These prisms cover the square faces so the resulting polyhedron has four equilateral triangles and four squares, making eight faces in total, an octahedron.^[4] Because its faces are all regular polygons and it is convex, the gyrobifastigium is a Johnson solid, indexed as $J_{26}$ .^[5]

The name of the gyrobifastigium comes from the Latin fastigium, meaning a sloping roof.^[6] In the standard naming convention of the Johnson solids, bi- means two solids connected at their bases, and gyro- means the two halves are twisted with respect to each other.^[4]

Cartesian coordinates for the gyrobifastigium with regular faces and unit edge lengths may easily be derived from the formula of the height of unit edge length ${\textstyle h={\frac {\sqrt {3}}{2}}}$ as follows: $\left(\pm {\frac {1}{2}},\pm {\frac {1}{2}},0\right),\left(0,\pm {\frac {1}{2}},{\frac {{\sqrt {3}}+1}{2}}\right),\left(\pm {\frac {1}{2}},0,-{\frac {{\sqrt {3}}+1}{2}}\right).$

Properties

To calculate the formula for the surface area and volume of a gyrobifastigium with regular faces and with edge length $a$ , one may adapt the corresponding formulae for the triangular prism. Its surface area $A$ can be obtained by summing the area of four equilateral triangles and four squares, whereas its volume $V$ by slicing it off into two triangular prisms and adding their volume. That is:^[4] ${\begin{aligned}A&=\left(4+{\sqrt {3}}\right)a^{2}\approx 5.73205a^{2},\\V&=\left({\frac {\sqrt {3}}{2}}\right)a^{3}\approx 0.86603a^{3}.\end{aligned}}$

Related figures

The Schmitt–Conway–Danzer biprism

The gyrobifastigium honeycomb

The Schmitt–Conway–Danzer biprism (also called a SCD prototile^[7]) is a polyhedron topologically equivalent to the gyrobifastigium, but with parallelogram and irregular triangle faces instead of squares and equilateral triangles. Like the gyrobifastigium, it can fill space, but only aperiodically or with a screw symmetry, not with a full three-dimensional group of symmetries. Thus, it provides a partial solution to the three-dimensional einstein problem.^[8]

The gyrated triangular prismatic honeycomb can be constructed by packing together large numbers of identical gyrobifastigiums. The gyrobifastigium is one of five convex polyhedra with regular faces capable of space-filling (the others being the cube, truncated octahedron, triangular prism, and hexagonal prism) and it is the only Johnson solid capable of doing so.^[1]^[2]

References

^ ^a ^b Alam, S. M. Nazrul; Haas, Zygmunt J. (2006), "Coverage and Connectivity in Three-dimensional Networks", Proceedings of the 12th Annual International Conference on Mobile Computing and Networking (MobiCom '06), New York, NY, USA: ACM, pp. 346–357, arXiv:cs/0609069, doi:10.1145/1161089.1161128, ISBN 1-59593-286-0, S2CID 3205780.
^ ^a ^b Kepler, Johannes (2010), The Six-Cornered Snowflake, Paul Dry Books, Footnote 18, p. 146, ISBN 9781589882850.
^ Darling, David (2004), The Universal Book of Mathematics: From Abracadabra to Zeno's Paradoxes, John Wiley & Sons, p. 169, ISBN 9780471667001.
^ ^a ^b ^c Berman, Martin (1971), "Regular-faced convex polyhedra", Journal of the Franklin Institute, 291 (5): 329–352, doi:10.1016/0016-0032(71)90071-8, MR 0290245.
^ Francis, Darryl (2013), "Johnson solids & their acronyms", Word Ways, 46 (3): 177.
^ Rich, Anthony (1875), "Fastigium", in Smith, William (ed.), A Dictionary of Greek and Roman Antiquities, London: John Murray, pp. 523–524.
^ Forcing Nonperiodicity With a Single Tile Joshua E. S. Socolar and Joan M. Taylor, 2011
^ Senechal, Marjorie (1996), "7.2 The SCD (Schmitt–Conway–Danzer) tile", Quasicrystals and Geometry, Cambridge University Press, pp. 209–213, ISBN 9780521575416.

External links

Weisstein, Eric W., "Gyrobifastigium" ("Johnson solid") at MathWorld.

[ah06-1] Alam, S. M. Nazrul; Haas, Zygmunt J. (2006), "Coverage and Connectivity in Three-dimensional Networks", Proceedings of the 12th Annual International Conference on Mobile Computing and Networking (MobiCom '06), New York, NY, USA: ACM, pp. 346–357, arXiv:cs/0609069, doi:10.1145/1161089.1161128, ISBN 1-59593-286-0, S2CID 3205780.

[kepler-2] Kepler, Johannes (2010), The Six-Cornered Snowflake, Paul Dry Books, Footnote 18, p. 146, ISBN 9781589882850.

[darling-3] Darling, David (2004), The Universal Book of Mathematics: From Abracadabra to Zeno's Paradoxes, John Wiley & Sons, p. 169, ISBN 9780471667001.

[berman-4] Berman, Martin (1971), "Regular-faced convex polyhedra", Journal of the Franklin Institute, 291 (5): 329–352, doi:10.1016/0016-0032(71)90071-8, MR 0290245.

[francis-5] Francis, Darryl (2013), "Johnson solids & their acronyms", Word Ways, 46 (3): 177.

[6] Rich, Anthony (1875), "Fastigium", in Smith, William (ed.), A Dictionary of Greek and Roman Antiquities, London: John Murray, pp. 523–524.

[7] Forcing Nonperiodicity With a Single Tile Joshua E. S. Socolar and Joan M. Taylor, 2011

[senechal-8] Senechal, Marjorie (1996), "7.2 The SCD (Schmitt–Conway–Danzer) tile", Quasicrystals and Geometry, Cambridge University Press, pp. 209–213, ISBN 9780521575416.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]