 120-cell |
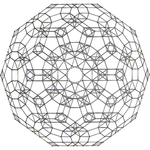 Cantellated 120-cell |
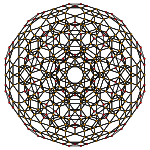 Cantellated 600-cell |
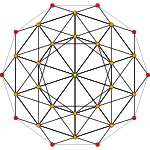 600-cell |
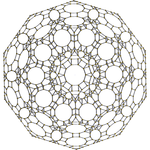 Cantitruncated 120-cell |
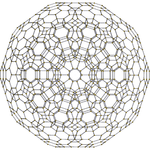 Cantitruncated 600-cell |
| Orthogonal projections in H3 Coxeter plane | ||
|---|---|---|
In four-dimensional geometry, a cantellated 120-cell is a convex uniform 4-polytope, being a cantellation (a 2nd order truncation) of the regular 120-cell.
There are four degrees of cantellations of the 120-cell including with permutations truncations. Two are expressed relative to the dual 600-cell.
Cantellated 120-cell
edit| Cantellated 120-cell | |
|---|---|
| Type | Uniform 4-polytope |
| Uniform index | 37 |
| Coxeter diagram | |
| Cells | 1920 total: 120 (3.4.5.4) 1200 (3.4.4) 600 (3.3.3.3) |
| Faces | 4800{3}+3600{4}+720{5} |
| Edges | 10800 |
| Vertices | 3600 |
| Vertex figure | wedge |
| Schläfli symbol | t0,2{5,3,3} |
| Symmetry group | H4, [3,3,5], order 14400 |
| Properties | convex |
The cantellated 120-cell is a uniform 4-polytope. It is named by its construction as a Cantellation operation applied to the regular 120-cell. It contains 1920 cells, including 120 rhombicosidodecahedra, 1200 triangular prisms, 600 octahedra. Its vertex figure is a wedge, with two rhombicosidodecahedra, two triangular prisms, and one octahedron meeting at each vertex.
Alternative names
edit- Cantellated 120-cell Norman Johnson
- Cantellated hecatonicosachoron / Cantellated dodecacontachoron / Cantellated polydodecahedron
- Small rhombated hecatonicosachoron (Acronym srahi) (George Olshevsky and Jonathan Bowers)[1]
- Ambo-02 polydodecahedron (John Conway)
Images
edit| H3 | A2 / B3 / D4 | A3 / B2 |
|---|---|---|
| [10] |
[6] |
[4] |
| Schlegel diagram. Pentagonal face are removed. |
Cantitruncated 120-cell
edit| Cantitruncated 120-cell | |
|---|---|
| Type | Uniform 4-polytope |
| Uniform index | 42 |
| Schläfli symbol | t0,1,2{5,3,3} |
| Coxeter diagram | |
| Cells | 1920 total: 120 (4.6.10) 1200 (3.4.4) 600 (3.6.6) |
| Faces | 9120: 2400{3}+3600{4}+ 2400{6}+720{10} |
| Edges | 14400 |
| Vertices | 7200 |
| Vertex figure | sphenoid |
| Symmetry group | H4, [3,3,5], order 14400 |
| Properties | convex |
The cantitruncated 120-cell is a uniform polychoron.
This 4-polytope is related to the regular 120-cell. The cantitruncation operation create new truncated tetrahedral cells at the vertices, and triangular prisms at the edges. The original dodecahedron cells are cantitruncated into great rhombicosidodecahedron cells.
The image shows the 4-polytope drawn as a Schlegel diagram which projects the 4-dimensional figure into 3-space, distorting the sizes of the cells. In addition, the decagonal faces are hidden, allowing us to see the elemented projected inside.
Alternative names
edit- Cantitruncated 120-cell Norman Johnson
- Cantitruncated hecatonicosachoron / Cantitruncated polydodecahedron
- Great rhombated hecatonicosachoron (Acronym grahi) (George Olshevsky and Jonthan Bowers)[2]
- Ambo-012 polydodecahedron (John Conway)
Images
edit| H3 | A2 / B3 / D4 | A3 / B2 |
|---|---|---|
| [10] |
[6] |
[4] |
| Centered on truncated icosidodecahedron cell with decagonal faces hidden. |
Cantellated 600-cell
edit| Cantellated 600-cell | |
|---|---|
| Type | Uniform 4-polytope |
| Uniform index | 40 |
| Schläfli symbol | t0,2{3,3,5} |
| Coxeter diagram | |
| Cells | 1440 total: 120 3.5.3.5 600 3.4.3.4 720 4.4.5 |
| Faces | 8640 total: (1200+2400){3} +3600{4}+1440{5} |
| Edges | 10800 |
| Vertices | 3600 |
| Vertex figure | isosceles triangular prism |
| Symmetry group | H4, [3,3,5], order 14400 |
| Properties | convex |
The cantellated 600-cell is a uniform 4-polytope. It has 1440 cells: 120 icosidodecahedra, 600 cuboctahedra, and 720 pentagonal prisms. Its vertex figure is an isosceles triangular prism, defined by one icosidodecahedron, two cuboctahedra, and two pentagonal prisms.
Alternative names
edit- Cantellated 600-cell Norman Johnson
- Cantellated hexacosichoron / Cantellated tetraplex
- Small rhombihexacosichoron (Acronym srix) (George Olshevsky and Jonathan Bowers)[3]
- Ambo-02 tetraplex (John Conway)
Construction
editThis 4-polytope has cells at 3 of 4 positions in the fundamental domain, extracted from the Coxeter diagram by removing one node at a time:
| Node | Order | Coxeter diagram |
Cell | Picture |
|---|---|---|---|---|
| 0 | 600 | Cantellated tetrahedron (Cuboctahedron) |
||
| 1 | 1200 | None (Degenerate triangular prism) |
||
| 2 | 720 | Pentagonal prism | ||
| 3 | 120 | Rectified dodecahedron (Icosidodecahedron) |
There are 1440 pentagonal faces between the icosidodecahedra and pentagonal prisms. There are 3600 squares between the cuboctahedra and pentagonal prisms. There are 2400 triangular faces between the icosidodecahedra and cuboctahedra, and 1200 triangular faces between pairs of cuboctahedra.
There are two classes of edges: 3-4-4, 3-4-5: 3600 have two squares and a triangle around it, and 7200 have one triangle, one square, and one pentagon.
Images
edit| H4 | - |
|---|---|
| [30] |
[20] |
| F4 | H3 |
| [12] |
[10] |
| A2 / B3 / D4 | A3 / B2 |
| [6] |
[4] |
| Stereographic projection with its 3600 green triangular faces and its 3600 blue square faces. |
Cantitruncated 600-cell
edit| Cantitruncated 600-cell | |
|---|---|
| Type | Uniform 4-polytope |
| Uniform index | 45 |
| Coxeter diagram | |
| Cells | 1440 total: 120 (5.6.6) 720 (4.4.5) 600 (4.6.6) |
| Faces | 8640: 3600{4}+1440{5}+ 3600{6} |
| Edges | 14400 |
| Vertices | 7200 |
| Vertex figure | sphenoid |
| Schläfli symbol | t0,1,2{3,3,5} |
| Symmetry group | H4, [3,3,5], order 14400 |
| Properties | convex |
The cantitruncated 600-cell is a uniform 4-polytope. It is composed of 1440 cells: 120 truncated icosahedra, 720 pentagonal prisms and 600 truncated octahedra. It has 7200 vertices, 14400 edges, and 8640 faces (3600 squares, 1440 pentagons, and 3600 hexagons). It has an irregular tetrahedral vertex figure, filled by one truncated icosahedron, one pentagonal prism and two truncated octahedra.
Alternative names
edit- Cantitruncated 600-cell (Norman Johnson)
- Cantitruncated hexacosichoron / Cantitruncated polydodecahedron
- Great rhombated hexacosichoron (acronym grix) (George Olshevsky and Jonathan Bowers)[4]
- Ambo-012 polytetrahedron (John Conway)
Images
edit| H3 | A2 / B3 / D4 | A3 / B2 |
|---|---|---|
| [10] |
[6] |
[4] |
Related polytopes
edit| H4 family polytopes | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 120-cell | rectified 120-cell |
truncated 120-cell |
cantellated 120-cell |
runcinated 120-cell |
cantitruncated 120-cell |
runcitruncated 120-cell |
omnitruncated 120-cell | ||||
| {5,3,3} | r{5,3,3} | t{5,3,3} | rr{5,3,3} | t0,3{5,3,3} | tr{5,3,3} | t0,1,3{5,3,3} | t0,1,2,3{5,3,3} | ||||
| 600-cell | rectified 600-cell |
truncated 600-cell |
cantellated 600-cell |
bitruncated 600-cell |
cantitruncated 600-cell |
runcitruncated 600-cell |
omnitruncated 600-cell | ||||
| {3,3,5} | r{3,3,5} | t{3,3,5} | rr{3,3,5} | 2t{3,3,5} | tr{3,3,5} | t0,1,3{3,3,5} | t0,1,2,3{3,3,5} | ||||
Notes
editReferences
edit- Convex uniform polychora based on the hecatonicosachoron (120-cell) and hexacosichoron (600-cell) - Model 37, George Olshevsky.
- Archimedisches Polychor Nr. 57 (cantellated 120-cell) Marco Möller's Archimedean polytopes in R4 (German)
- Kaleidoscopes: Selected Writings of H.S.M. Coxeter, edited by F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6
- (Paper 22) H.S.M. Coxeter, Regular and Semi Regular Polytopes I, [Math. Zeit. 46 (1940) 380-407, MR 2,10]
- (Paper 23) H.S.M. Coxeter, Regular and Semi-Regular Polytopes II, [Math. Zeit. 188 (1985) 559-591]
- (Paper 24) H.S.M. Coxeter, Regular and Semi-Regular Polytopes III, [Math. Zeit. 200 (1988) 3-45]
- J.H. Conway and M.J.T. Guy: Four-Dimensional Archimedean Polytopes, Proceedings of the Colloquium on Convexity at Copenhagen, page 38 und 39, 1965
- N.W. Johnson: The Theory of Uniform Polytopes and Honeycombs, Ph.D. Dissertation, University of Toronto, 1966
- Four-dimensional Archimedean Polytopes (German), Marco Möller, 2004 PhD dissertation [1] Archived 2005-03-22 at the Wayback Machine m63 m61 m56
- Convex uniform polychora based on the hecatonicosachoron (120-cell) and hexacosichoron (600-cell) - Model 40, 42, 45, George Olshevsky.
- Klitzing, Richard. "4D uniform polytopes (polychora)". o3x3o5x - srahi, o3x3x5x - grahi, x3o3x5o - srix, x3x3x5o - grix
External links
edit- Four-Dimensional Polytope Projection Barn Raisings (A Zometool construction of the cantitruncated 120-cell), George W. Hart
- Renaissance Banff 2005 Zome Project: a Zome model of a 3D orthogonal projection of the cantellated 600-cell.
- H4 uniform polytopes with coordinates: rr{3,3,5} rr{5,3,3} tr{3,3,5} tr{5,3,3}