User:Tomruen/Uniform polyteron verf
Vertex figures (as Schlegel diagrams) for uniform polyterons, uniform honeycombs (Euclidean and hyperbolic). (Excluding prismatic forms, and nonwythoffian forms)
Tables are expanded for finite and infinite forms (spherical/Euclidean/hyperbolic) for completeness, not that I expect ever to include all of the hyperbolic forms! (Compare to 4-polytopes: Talk:Vertex figure/polychoron)
Spherical
editThere are three fundamental affine Coxeter groups that generate regular and uniform tessellations on the 3-sphere:
| # | Coxeter group | Coxeter graph | |
|---|---|---|---|
| 1 | A5 | [34] | |
| 2 | B5 | [4,33] | |
| 3 | D5 | [32,1,1] | |
In addition there are prismatic groups:
Uniform prismatic forms:
| # | Coxeter groups | Coxeter graph | |
|---|---|---|---|
| 1 | A4 × A1 | [3,3,3] × [ ] | |
| 2 | B4 × A1 | [4,3,3] × [ ] | |
| 3 | F4 × A1 | [3,4,3] × [ ] | |
| 4 | H4 × A1 | [5,3,3] × [ ] | |
| 5 | D4 × A1 | [31,1,1] × [ ] | |
Uniform duoprism prismatic forms:
| Coxeter groups | Coxeter graph | |
|---|---|---|
| I2(p) × I2(q) × A1 | [p] × [q] × [ ] | |
Uniform duoprismatic forms:
| # | Coxeter groups | Coxeter graph | |
|---|---|---|---|
| 1 | A3 × I2(p) | [3,3] × [p] | |
| 2 | B3 × I2(p) | [4,3] × [p] | |
| 3. | H3 × I2(p) | [5,3] × [p] | |
Euclidean
editThere are five fundamental affine Coxeter groups that generate regular and uniform tessellations in 4-space:
| # | Coxeter group | Coxeter-Dynkin diagram | |
|---|---|---|---|
| 1 | A~4 | [(3,3,3,3,3)] | |
| 2 | B~4 | [4,3,3,4] | |
| 3 | C~4 | [4,3,31,1] | |
| 4 | D~4 | [31,1,1,1] | |
| 5 | F~4 | [3,4,3,3] | |
In addition there are prismatic groups:
Duoprismatic forms
- B~2xB~2: [4,4]x[4,4] = [4,3,3,4]










 =
= 







 (Same as tesseractic honeycomb family)
(Same as tesseractic honeycomb family) - B~2xH~2: [4,4]x[6,3]











- H~2xH~2: [6,3]x[6,3]











- A~2xB~2: [3[3]]]x[4,4]








 (Same forms as [6,3]x[4,4])
(Same forms as [6,3]x[4,4]) - A~2xH~2: [3[3]]]x[6,3]








 (Same forms as [6,3]x[6,3])
(Same forms as [6,3]x[6,3]) - A~2xA~2: [3[3]]]x[3[3]]






 (Same forms as [6,3]x[6,3])
(Same forms as [6,3]x[6,3])
Prismatic forms
- B~3xI~1: [4,3,4]x[∞]











- D~3xI~1: [4,31,1]x[∞]









- A~3xI~1: [3[4]]x[∞]







Hyperbolic
edit| 1 | [5,3,3,3] | |
|---|---|---|
| 2 | [5,3,3,4] | |
| 3 | [5,3,3,5] | |
| 4 | [5,3,31,1] | |
| 5 | [(4,3,3,3,3)] |
Linear Coxeter graphs
editThere are 31 truncation forms for each group, or 19 subgrouped as half-families as given below (with 7 overlapped).
Summary chart: File:Uniform polyteron vertex figure chart.png
| # | Operation Coxeter-Dynkin |
General {p,q,r,s} |
Spherical | Euclidean | Hyperbolic | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 5-simplex [3,3,3,3] |
5-cube [4,3,3,3] |
5-orthoplex [3,3,3,4] |
[4,3,3,4] |
[3,4,3,3] |
[3,3,4,3] |
[3,3,3,5] |
[5,3,3,3] |
[4,3,3,5] |
[5,3,3,4] |
[5,3,3,5] | |||
| 1 | Regular |
{q,r,s}:(p) |  {3,3,3}:(3) |
 {3,3,3}:(4) |
 {3,3,4}:(3) |
 {3,3,4}:(4) |
 {4,3,3}:(3) |
{3,4,3}:(3) |
 {3,3,5}:(3) |
{3,3,3}:(5) |
 {3,3,5}:(4) |
 {3,3,4}:(5) |
 {3,3,5}:(5) |
| 2 | Rectified |
 {r,s}-prism |

|

|

|

| |||||||
| 3 | Birectified |
 p-s duoprism |
 3-3 duoprism |
 3-4 duoprism |
 3-4 duoprism |
 4-4 duoprism |
 3-3 duoprism |
 3-3 duoprism | |||||
| 4 | Truncated |
 {r,s}-pyramid |

|

|

|
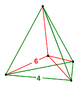
| |||||||
| 5 | Bitruncated |

|

|

|

|

|

|

| |||||
| 6 | Cantellated |
 s-prism-wedge |

|

|

|

| |||||||
| 7 | Bicantellated |

|

|

|

|

|

|

| |||||
| 8 | Runcinated |

|

|

|

|

| |||||||
| 9 | Stericated |
 {q,r}-{r,q} antiprism |

|
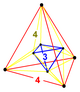
|

|

|

|

| |||||
| 10 | Cantitruncated |

|

|

|

| ||||||||
| 11 | Bicantitruncated |

|

|

|

| ||||||||
| 12 | Runcitruncated |
 wedge-pyramid |

|

|

| ||||||||
| 13 | Steritruncated |

|

|

|

| ||||||||
| 14 | Runcicantellated |

|

|
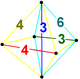
|
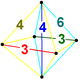
| ||||||||
| 15 | Stericantellated |

|

|

|

| ||||||||
| 16 | Runcicantitruncated |

|

|

|

| ||||||||
| 17 | Stericantitruncated |

|

|

|

| ||||||||
| 18 | Steriruncitruncated |

|

|
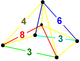
|

| ||||||||
| 19 | Omnitruncated |
 Irr. 5-simplex |

|

|

|
||||||||
| 20 | Alternated regular |
t1{3,3,p} |  t1{3,3,3} |
 t1{3,3,4} |
|||||||||
Bifurcating Coxeter graphs
editThere are 23 forms from each family, with 15 repeated from the linear [4,3,3,s] families above.
| # | Operation Coxeter-Dynkin |
Linear equiv | General | Spherical | Euclidean | Hyperbolic |
|---|---|---|---|---|---|---|
| [s,3,31,1] |
[3,3,31,1] |
[4,3,31,1] |
[5,3,31,1] | |||
| 1 | t1{3,3,s} |  t1{3,3,3} |
t1{3,3,4} | t1{3,3,5} | ||
| 2 | 
|
|||||
| 3 | 
| |||||
| 4 | 
| |||||
| 5 | 
|
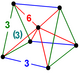
| ||||
| 6 | 
| |||||
| 7 | 
| |||||
| 8 | 
| |||||
| 9 | 
| |||||
| 10 | 
| |||||
| 11 | 
| |||||
| 12 | 
| |||||
| 13 | 
| |||||
| 14 | ||||||
| 15 | ||||||
| 16 | ||||||
| 17 | ||||||
| 18 | ||||||
| 19 | ||||||
| 20 | ||||||
| 21 | ||||||
| 22 | ||||||
| 23 | 
|
Trifurcating Coxeter graphs
editThere are 9 forms:
| Operation Coxeter-Dynkin |
Euclidean |
|---|---|
| Coxeter group | [31,1,1,1] |
Cyclic Coxeter graphs
editThere are 7 forms in the first cycle family, and 19 forms in the second cyclic family:
| # | General | Euclidean | Hyperbolic | |
|---|---|---|---|---|
| [(p,3,3,3,3)] |
[(3,3,3,3,3)] |
[(4,3,3,3,3)] | ||
| 1 | ||||
| 2 | ||||
| 3 | ||||
| 4 | ||||
| 5 | ||||
| 6 | ||||
| 7 | 
|