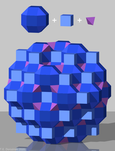
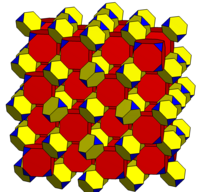
Tetrahedral-octahedral honeycomb
| Alternated cubic honeycomb | |
|---|---|
 
| |
| Type | Uniform honeycomb |
| Family | Alternated hypercubic honeycomb Simplectic honeycomb |
| Indexing[1] | J21,31,51, A2 W9, G1 |
| Schläfli symbols | h{4,3,4} {3[4]} ht0,3{4,3,4} h{4,4}h{∞} ht0,2{4,4}h{∞} h{∞}h{∞}h{∞} s{∞}s{∞}s{∞} |
| Coxeter diagrams | |
| Cells | {3,3} {3,4} |
| Faces | triangle {3} |
| Edge figure | [{3,3}.{3,4}]2 (rectangle) |
| Vertex figure |  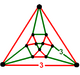  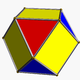 (cuboctahedron) |
| Symmetry group | Fm3m (225) |
| Coxeter group | , [4,31,1] |
| Dual | Dodecahedrille rhombic dodecahedral honeycomb Cell: 
|
| Properties | vertex-transitive, edge-transitive, quasiregular honeycomb |
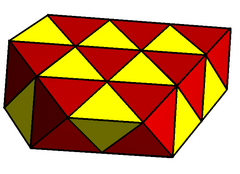
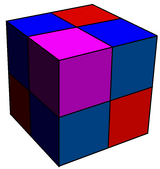
The tetrahedral-octahedral honeycomb, alternated cubic honeycomb is a quasiregular space-filling tessellation (or honeycomb) in Euclidean 3-space. It is composed of alternating regular octahedra and tetrahedra in a ratio of 1:2.
Other names include half cubic honeycomb, half cubic cellulation, or tetragonal disphenoidal cellulation. John Horton Conway calls this honeycomb a tetroctahedrille, and its dual a dodecahedrille.
R. Buckminster Fuller combines the two words octahedron and tetrahedron into octet truss, a rhombohedron consisting of one octahedron (or two square pyramids) and two opposite tetrahedra.
It is vertex-transitive with 8 tetrahedra and 6 octahedra around each vertex. It is edge-transitive with 2 tetrahedra and 2 octahedra alternating on each edge.
A geometric honeycomb is a space-filling of polyhedral or higher-dimensional cells, so that there are no gaps. It is an example of the more general mathematical tiling or tessellation in any number of dimensions.
Honeycombs are usually constructed in ordinary Euclidean ("flat") space, like the convex uniform honeycombs. They may also be constructed in non-Euclidean spaces, such as hyperbolic uniform honeycombs. Any finite uniform polytope can be projected to its circumsphere to form a uniform honeycomb in spherical space.
It is part of an infinite family of uniform honeycombs called alternated hypercubic honeycombs, formed as an alternation of a hypercubic honeycomb and being composed of demihypercube and cross-polytope facets. It is also part of another infinite family of uniform honeycombs called simplectic honeycombs.
In this case of 3-space, the cubic honeycomb is alternated, reducing the cubic cells to tetrahedra, and the deleted vertices create octahedral voids. As such it can be represented by an extended Schläfli symbol h{4,3,4} as containing half the vertices of the {4,3,4} cubic honeycomb.
There is a similar honeycomb called gyrated tetrahedral-octahedral honeycomb which has layers rotated 60 degrees so half the edges have neighboring rather than alternating tetrahedra and octahedra.
The tetrahedral-octahedral honeycomb can have its symmetry doubled by placing tetrahedra on the octahedral cells, creating a nonuniform honeycomb consisting of tetrahedra and octahedra (as triangular antiprisms). Its vertex figure is an order-3 truncated triakis tetrahedron. This honeycomb is the dual of the triakis truncated tetrahedral honeycomb, with triakis truncated tetrahedral cells.
Cartesian coordinates
editFor an alternated cubic honeycomb, with edges parallel to the axes and with an edge length of 1, the Cartesian coordinates of the vertices are: (For all integral values: i,j,k with i+j+k even)
- (i, j, k)

Symmetry
editThere are two reflective constructions and many alternated cubic honeycomb ones; examples:
| Symmetry | , [4,31,1] = ½, [1+,4,3,4] |
, [3[4]] = ½, [1+,4,31,1] |
[[(4,3,4,2+)]] | [(4,3,4,2+)] |
|---|---|---|---|---|
| Space group | Fm3m (225) | F43m (216) | I43m (217) | P43m (215) |
| Image | 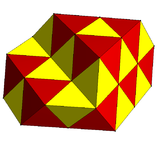
|
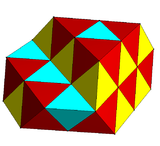
|
||
| Types of tetrahedra | 1 | 2 | 3 | 4 |
| Coxeter diagram |
Alternated cubic honeycomb slices
editThe alternated cubic honeycomb can be sliced into sections, where new square faces are created from inside of the octahedron. Each slice will contain up and downward facing square pyramids and tetrahedra sitting on their edges. A second slice direction needs no new faces and includes alternating tetrahedral and octahedral. This slab honeycomb is a scaliform honeycomb rather than uniform because it has nonuniform cells.

|
|
Projection by folding
editThe alternated cubic honeycomb can be orthogonally projected into the planar square tiling by a geometric folding operation that maps one pairs of mirrors into each other. The projection of the alternated cubic honeycomb creates two offset copies of the square tiling vertex arrangement of the plane:
| Coxeter group |
||
|---|---|---|
| Coxeter diagram |
||
| Image | 
|

|
| Name | alternated cubic honeycomb | square tiling |
A3/D3 lattice
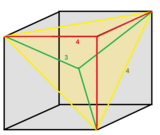
editIts vertex arrangement represents an A3 lattice or D3 lattice.[2][3] This lattice is known as the face-centered cubic lattice in crystallography and is also referred to as the cubic close packed lattice as its vertices are the centers of a close-packing with equal spheres that achieves the highest possible average density. The tetrahedral-octahedral honeycomb is the 3-dimensional case of a simplectic honeycomb. Its Voronoi cell is a rhombic dodecahedron, the dual of the cuboctahedron vertex figure for the tet-oct honeycomb.
The D+
3 packing can be constructed by the union of two D3 (or A3) lattices. The D+
n packing is only a lattice for even dimensions. The kissing number is 22=4, (2n-1 for n<8, 240 for n=8, and 2n(n-1) for n>8).[4]




 ∪
∪ 




The A*
3 or D*
3 lattice (also called A4
3 or D4
3) can be constructed by the union of all four A3 lattices, and is identical to the vertex arrangement of the disphenoid tetrahedral honeycomb, dual honeycomb of the uniform bitruncated cubic honeycomb:[5] It is also the body centered cubic, the union of two cubic honeycombs in dual positions.




 ∪
∪ 



 ∪
∪ 



 ∪
∪ 



 = dual of
= dual of 



 =
= 





 ∪
∪ 





 .
.
The kissing number of the D*
3 lattice is 8[6] and its Voronoi tessellation is a bitruncated cubic honeycomb, ![]()
![]()
![]() , containing all truncated octahedral Voronoi cells,
, containing all truncated octahedral Voronoi cells, ![]()
![]()
![]()
![]()
![]() .[7]
.[7]
Related honeycombs
editC3 honeycombs
editThe [4,3,4], ![]()
![]()
![]()
![]()
![]()
![]()
![]() , Coxeter group generates 15 permutations of uniform honeycombs, 9 with distinct geometry including the alternated cubic honeycomb. The expanded cubic honeycomb (also known as the runcinated tesseractic honeycomb) is geometrically identical to the cubic honeycomb.
, Coxeter group generates 15 permutations of uniform honeycombs, 9 with distinct geometry including the alternated cubic honeycomb. The expanded cubic honeycomb (also known as the runcinated tesseractic honeycomb) is geometrically identical to the cubic honeycomb.
| C3 honeycombs | |||||
|---|---|---|---|---|---|
| Space group |
Fibrifold | Extended symmetry |
Extended diagram |
Order | Honeycombs |
| Pm3m (221) |
4−:2 | [4,3,4] | ×1 | ||
| Fm3m (225) |
2−:2 | [1+,4,3,4] ↔ [4,31,1] |
↔ |
Half | |
| I43m (217) |
4o:2 | [[(4,3,4,2+)]] | Half × 2 | ||
| Fd3m (227) |
2+:2 | [[1+,4,3,4,1+]] ↔ [[3[4]]] |
↔ |
Quarter × 2 | |
| Im3m (229) |
8o:2 | [[4,3,4]] | ×2 | ||
B3 honeycombs
editThe [4,31,1], ![]()
![]()
![]()
![]()
![]() , Coxeter group generates 9 permutations of uniform honeycombs, 4 with distinct geometry including the alternated cubic honeycomb.
, Coxeter group generates 9 permutations of uniform honeycombs, 4 with distinct geometry including the alternated cubic honeycomb.
| B3 honeycombs | |||||
|---|---|---|---|---|---|
| Space group |
Fibrifold | Extended symmetry |
Extended diagram |
Order | Honeycombs |
| Fm3m (225) |
2−:2 | [4,31,1] ↔ [4,3,4,1+] |
↔ |
×1 | |
| Fm3m (225) |
2−:2 | <[1+,4,31,1]> ↔ <[3[4]]> |
↔ |
×2 | |
| Pm3m (221) |
4−:2 | <[4,31,1]> | ×2 | ||
A3 honeycombs
editThis honeycomb is one of five distinct uniform honeycombs[8] constructed by the Coxeter group. The symmetry can be multiplied by the symmetry of rings in the Coxeter–Dynkin diagrams:
| A3 honeycombs | ||||||
|---|---|---|---|---|---|---|
| Space group |
Fibrifold | Square symmetry |
Extended symmetry |
Extended diagram |
Extended group |
Honeycomb diagrams |
| F43m (216) |
1o:2 | a1 |
[3[4]] | (None) | ||
| Fm3m (225) |
2−:2 | d2 |
<[3[4]]> ↔ [4,31,1] |
↔ |
×21 ↔ |
|
| Fd3m (227) |
2+:2 | g2 |
[[3[4]]] or [2+[3[4]]] |
↔ |
×22 | |
| Pm3m (221) |
4−:2 | d4 |
<2[3[4]]> ↔ [4,3,4] |
↔ |
×41 ↔ |
|
| I3 (204) |
8−o | r8 |
[4[3[4]]]+ ↔ [[4,3+,4]] |
↔ |
½×8 ↔ ½×2 |
|
| Im3m (229) |
8o:2 | [4[3[4]]] ↔ [[4,3,4]] |
×8 ↔ ×2 |
|||
Quasiregular honeycombs
edit| Quasiregular polychora and honeycombs: h{4,p,q} | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Space | Finite | Affine | Compact | Paracompact | |||||||
| Schläfli symbol |
h{4,3,3} | h{4,3,4} | h{4,3,5} | h{4,3,6} | h{4,4,3} | h{4,4,4} | |||||
| Coxeter diagram |
|||||||||||
| Image | 
|

|

|

| |||||||
| Vertex figure r{p,3} |
 |
 |
 |
 |
 |
 | |||||
Cantic cubic honeycomb
edit| Cantic cubic honeycomb | |
|---|---|
| Type | Uniform honeycomb |
| Schläfli symbol | h2{4,3,4} |
| Coxeter diagrams | |
| Cells | t{3,4} r{4,3} t{3,3} |
| Faces | triangle {3} square {4} hexagon {6} |
| Vertex figure | 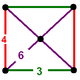 rectangular pyramid |
| Coxeter groups | [4,31,1], [3[4]], |
| Symmetry group | Fm3m (225) |
| Dual | half oblate octahedrille Cell: 
|
| Properties | vertex-transitive |
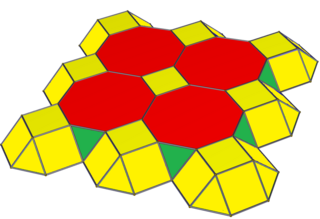
The cantic cubic honeycomb, cantic cubic cellulation or truncated half cubic honeycomb is a uniform space-filling tessellation (or honeycomb) in Euclidean 3-space. It is composed of truncated octahedra, cuboctahedra and truncated tetrahedra in a ratio of 1:1:2. Its vertex figure is a rectangular pyramid.
John Horton Conway calls this honeycomb a truncated tetraoctahedrille, and its dual half oblate octahedrille.
Symmetry
editIt has two different uniform constructions. The construction can be seen with alternately colored truncated tetrahedra.
| Symmetry | [4,31,1], =<[3[4]]> |
[3[4]], |
|---|---|---|
| Space group | Fm3m (225) | F43m (216) |
| Coloring | 
|
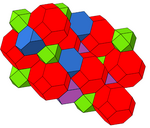
|
| Coxeter | ||
| Vertex figure | 
|
|
Related honeycombs
editIt is related to the cantellated cubic honeycomb. Rhombicuboctahedra are reduced to truncated octahedra, and cubes are reduced to truncated tetrahedra.
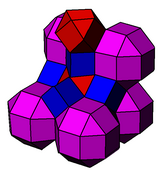 cantellated cubic |
 Cantic cubic |
rr{4,3}, r{4,3}, {4,3} |
t{3,4}, r{4,3}, t{3,3} |
Runcic cubic honeycomb
edit| Runcic cubic honeycomb | |
|---|---|
| Type | Uniform honeycomb |
| Schläfli symbol | h3{4,3,4} |
| Coxeter diagrams | |
| Cells | rr{4,3} {4,3} {3,3} |
| Faces | triangle {3} square {4} |
| Vertex figure |  triangular frustum |
| Coxeter group | , [4,31,1] |
| Symmetry group | Fm3m (225) |
| Dual | quarter cubille Cell: 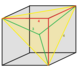
|
| Properties | vertex-transitive |
The runcic cubic honeycomb or runcic cubic cellulation is a uniform space-filling tessellation (or honeycomb) in Euclidean 3-space. It is composed of rhombicuboctahedra, cubes, and tetrahedra in a ratio of 1:1:2. Its vertex figure is a triangular frustum, with a tetrahedron on one end, cube on the opposite end, and three rhombicuboctahedra around the trapezoidal sides.
John Horton Conway calls this honeycomb a 3-RCO-trille, and its dual quarter cubille.
Quarter cubille
editThe dual of a runcic cubic honeycomb is called a quarter cubille, with Coxeter diagram ![]()
![]()
![]()
![]()
![]()
![]()
![]() , with faces in 2 of 4 hyperplanes of the , [4,31,1] symmetry fundamental domain.
, with faces in 2 of 4 hyperplanes of the , [4,31,1] symmetry fundamental domain.
Cells can be seen as 1/4 of dissected cube, using 4 vertices and the center. Four cells exist around 6 edges, and 3 cells around 3 edges.
Related honeycombs
editIt is related to the runcinated cubic honeycomb, with quarter of the cubes alternated into tetrahedra, and half expanded into rhombicuboctahedra.
 Runcinated cubic |
 Runcic cubic |
| {4,3}, {4,3}, {4,3}, {4,3} |
h{4,3}, rr{4,3}, {4,3} |
This honeycomb can be divided on truncated square tiling planes, using the octagons centers of the rhombicuboctahedra, creating square cupolae. This scaliform honeycomb is represented by Coxeter diagram ![]()
![]()
![]()
![]()
![]()
![]()
![]() , and symbol s3{2,4,4}, with coxeter notation symmetry [2+,4,4].
, and symbol s3{2,4,4}, with coxeter notation symmetry [2+,4,4].
Runcicantic cubic honeycomb
edit| Runcicantic cubic honeycomb | |
|---|---|
| Type | Uniform honeycomb |
| Schläfli symbol | h2,3{4,3,4} |
| Coxeter diagrams | |
| Cells | tr{4,3} t{4,3} t{3,3} |
| Faces | triangle {3} square {4} hexagon {6} octagon {8} |
| Vertex figure |  mirrored sphenoid |
| Coxeter group | , [4,31,1] |
| Symmetry group | Fm3m (225) |
| Dual | half pyramidille Cell: 
|
| Properties | vertex-transitive |
The runcicantic cubic honeycomb or runcicantic cubic cellulation is a uniform space-filling tessellation (or honeycomb) in Euclidean 3-space. It is composed of truncated cuboctahedra, truncated cubes and truncated tetrahedra in a ratio of 1:1:2, with a mirrored sphenoid vertex figure. It is related to the runcicantellated cubic honeycomb.
John Horton Conway calls this honeycomb a f-tCO-trille, and its dual half pyramidille.
Half pyramidille
editThe dual to the runcitruncated cubic honeycomb is called a half pyramidille, with Coxeter diagram ![]()
![]()
![]()
![]()
![]()
![]()
![]() . Faces exist in 3 of 4 hyperplanes of the [4,31,1], Coxeter group.
. Faces exist in 3 of 4 hyperplanes of the [4,31,1], Coxeter group.
Cells are irregular pyramids and can be seen as 1/12 of a cube, or 1/24 of a rhombic dodecahedron, each defined with three corner and the cube center.
Related skew apeirohedra
editA related uniform skew apeirohedron exists with the same vertex arrangement, but triangles and square removed. It can be seen as truncated tetrahedra and truncated cubes augmented together.
Related honeycombs
edit Runcicantic cubic |
 Runcicantellated cubic |
Gyrated tetrahedral-octahedral honeycomb
edit| Gyrated tetrahedral-octahedral honeycomb | |
|---|---|
| Type | convex uniform honeycomb |
| Coxeter diagrams | |
| Schläfli symbols | h{4,3,4}:g h{6,3}h{∞} s{3,6}h{∞} s{3[3]}h{∞} |
| Cells | {3,3} {3,4} |
| Faces | triangle {3} |
| Vertex figure |  triangular orthobicupola G3.4.3.4 |
| Space group | P63/mmc (194) [3,6,2+,∞] |
| Dual | trapezo-rhombic dodecahedral honeycomb |
| Properties | vertex-transitive |
The gyrated tetrahedral-octahedral honeycomb or gyrated alternated cubic honeycomb is a space-filling tessellation (or honeycomb) in Euclidean 3-space made up of octahedra and tetrahedra in a ratio of 1:2.
It is vertex-uniform with 8 tetrahedra and 6 octahedra around each vertex.
It is not edge-uniform. All edges have 2 tetrahedra and 2 octahedra, but some are alternating, and some are paired.
It can be seen as reflective layers of this layer honeycomb:

|
Construction by gyration
editThis is a less symmetric version of another honeycomb, tetrahedral-octahedral honeycomb, in which each edge is surrounded by alternating tetrahedra and octahedra. Both can be considered as consisting of layers one cell thick, within which the two kinds of cell strictly alternate. Because the faces on the planes separating these layers form a regular pattern of triangles, adjacent layers can be placed so that each octahedron in one layer meets a tetrahedron in the next layer, or so that each cell meets a cell of its own kind (the layer boundary thus becomes a reflection plane). The latter form is called gyrated.
The vertex figure is called a triangular orthobicupola, compared to the tetrahedral-octahedral honeycomb whose vertex figure cuboctahedron in a lower symmetry is called a triangular gyrobicupola, so the gyro- prefix is reversed in usage.
| Honeycomb | Gyrated tet-oct | Reflective tet-oct |
|---|---|---|
| Image | 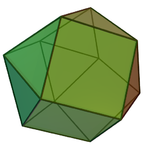
|

|
| Name | triangular orthobicupola | triangular gyrobicupola |
| Vertex figure | 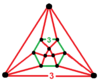
|
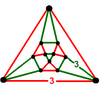
|
| Symmetry | D3h, order 12 |
D3d, order 12 (Oh, order 48) |
Construction by alternation
edit
The geometry can also be constructed with an alternation operation applied to a hexagonal prismatic honeycomb. The hexagonal prism cells become octahedra and the voids create triangular bipyramids which can be divided into pairs of tetrahedra of this honeycomb. This honeycomb with bipyramids is called a ditetrahedral-octahedral honeycomb. There are 3 Coxeter-Dynkin diagrams, which can be seen as 1, 2, or 3 colors of octahedra:
Gyroelongated alternated cubic honeycomb
edit| Gyroelongated alternated cubic honeycomb | |
|---|---|
| Type | Uniform honeycomb |
| Schläfli symbol | h{4,3,4}:ge {3,6}h1{∞} |
| Coxeter diagram | |
| Cells | {3,3} {3,4} (3.4.4) |
| Faces | triangle {3} square {4} |
| Vertex figure | 
|
| Space group | P63/mmc (194) [3,6,2+,∞] |
| Properties | vertex-transitive |
The gyroelongated alternated cubic honeycomb or elongated triangular antiprismatic cellulation is a space-filling tessellation (or honeycomb) in Euclidean 3-space. It is composed of octahedra, triangular prisms, and tetrahedra in a ratio of 1:2:2.
It is vertex-transitive with 3 octahedra, 4 tetrahedra, 6 triangular prisms around each vertex.
It is one of 28 convex uniform honeycombs.
The elongated alternated cubic honeycomb has the same arrangement of cells at each vertex, but the overall arrangement differs. In the elongated form, each prism meets a tetrahedron at one of its triangular faces and an octahedron at the other; in the gyroelongated form, the prism meets the same kind of deltahedron at each end.
Elongated alternated cubic honeycomb
edit| Elongated alternated cubic honeycomb | |
|---|---|
| Type | Uniform honeycomb |
| Schläfli symbol | h{4,3,4}:e {3,6}g1{∞} |
| Cells | {3,3} {3,4} (3.4.4) |
| Faces | triangle {3} square {4} |
| Vertex figure |  triangular cupola joined to isosceles hexagonal pyramid |
| Symmetry group | [6,(3,2+,∞,2+)] ? |
| Properties | vertex-transitive |
The elongated alternated cubic honeycomb or elongated triangular gyroprismatic cellulation is a space-filling tessellation (or honeycomb) in Euclidean 3-space. It is composed of octahedra, triangular prisms, and tetrahedra in a ratio of 1:2:2.
It is vertex-transitive with 3 octahedra, 4 tetrahedra, 6 triangular prisms around each vertex. Each prism meets an octahedron at one end and a tetrahedron at the other.
It is one of 28 convex uniform honeycombs.
It has a gyrated form called the gyroelongated alternated cubic honeycomb with the same arrangement of cells at each vertex.
See also
editNotes
edit- ^ For cross-referencing, they are given with list indices from Andreini (1-22), Williams(1-2,9-19), Johnson (11-19, 21-25, 31-34, 41-49, 51-52, 61-65), and Grünbaum(1-28).
- ^ "The Lattice D3".
- ^ "The Lattice A3".
- ^ Conway (1998), p. 119
- ^ "The Lattice D3".
- ^ Conway (1998), p. 120
- ^ Conway (1998), p. 466
- ^ [1], OEIS sequence A000029 6-1 cases, skipping one with zero marks
References
edit- John H. Conway, Heidi Burgiel, Chaim Goodman-Strauss, (2008) The Symmetries of Things, ISBN 978-1-56881-220-5 (Chapter 21, Naming the Archimedean and Catalan polyhedra and tilings, Architectonic and Catoptric tessellations, p 292–298, includes all the nonprismatic forms)
- George Olshevsky, Uniform Panoploid Tetracombs, Manuscript (2006) (Complete list of 11 convex uniform tilings, 28 convex uniform honeycombs, and 143 convex uniform tetracombs)
- Branko Grünbaum, Uniform tilings of 3-space. Geombinatorics 4(1994), 49 - 56.
- Norman Johnson Uniform Polytopes, Manuscript (1991)
- Williams, Robert (1979). The Geometrical Foundation of Natural Structure: A Source Book of Design. Dover Publications, Inc. ISBN 0-486-23729-X.
- Critchlow, Keith (1970). Order in Space: A design source book. Viking Press. ISBN 0-500-34033-1.
- Kaleidoscopes: Selected Writings of H.S.M. Coxeter, edited by F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6 [2]
- (Paper 22) H.S.M. Coxeter, Regular and Semi Regular Polytopes I, [Math. Zeit. 46 (1940) 380–407, MR 2,10] (1.9 Uniform space-fillings)
- (Paper 24) H.S.M. Coxeter, Regular and Semi-Regular Polytopes III, [Math. Zeit. 200 (1988) 3-45]
- A. Andreini, Sulle reti di poliedri regolari e semiregolari e sulle corrispondenti reti correlative (On the regular and semiregular nets of polyhedra and on the corresponding correlative nets), Mem. Società Italiana della Scienze, Ser.3, 14 (1905) 75–129.
- D. M. Y. Sommerville, An Introduction to the Geometry of n Dimensions. New York, E. P. Dutton, 1930. 196 pp. (Dover Publications edition, 1958) Chapter X: The Regular Polytopes
- Conway JH, Sloane NJH (1998). Sphere Packings, Lattices and Groups (3rd ed.). Springer. ISBN 0-387-98585-9.
External links
edit- Architectural design made with Tetrahedrons and regular Pyramids based square.(2003) Archived 2016-03-04 at the Wayback Machine
- Klitzing, Richard. "3D Euclidean Honeycombs x3o3o *b4o - octet - O21".
- Uniform Honeycombs in 3-Space: 11-Octet
| Space | Family | / / | ||||
|---|---|---|---|---|---|---|
| E2 | Uniform tiling | 0[3] | δ3 | hδ3 | qδ3 | Hexagonal |
| E3 | Uniform convex honeycomb | 0[4] | δ4 | hδ4 | qδ4 | |
| E4 | Uniform 4-honeycomb | 0[5] | δ5 | hδ5 | qδ5 | 24-cell honeycomb |
| E5 | Uniform 5-honeycomb | 0[6] | δ6 | hδ6 | qδ6 | |
| E6 | Uniform 6-honeycomb | 0[7] | δ7 | hδ7 | qδ7 | 222 |
| E7 | Uniform 7-honeycomb | 0[8] | δ8 | hδ8 | qδ8 | 133 • 331 |
| E8 | Uniform 8-honeycomb | 0[9] | δ9 | hδ9 | qδ9 | 152 • 251 • 521 |
| E9 | Uniform 9-honeycomb | 0[10] | δ10 | hδ10 | qδ10 | |
| E10 | Uniform 10-honeycomb | 0[11] | δ11 | hδ11 | qδ11 | |
| En-1 | Uniform (n-1)-honeycomb | 0[n] | δn | hδn | qδn | 1k2 • 2k1 • k21 |