In the mathematical field of set theory, an ultrafilter on a set is a maximal filter on the set In other words, it is a collection of subsets of that satisfies the definition of a filter on and that is maximal with respect to inclusion, in the sense that there does not exist a strictly larger collection of subsets of that is also a filter. (In the above, by definition a filter on a set does not contain the empty set.) Equivalently, an ultrafilter on the set can also be characterized as a filter on with the property that for every subset of either or its complement belongs to the ultrafilter.
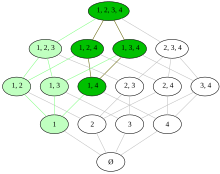
Ultrafilters on sets are an important special instance of ultrafilters on partially ordered sets, where the partially ordered set consists of the power set and the partial order is subset inclusion This article deals specifically with ultrafilters on a set and does not cover the more general notion.
There are two types of ultrafilter on a set. A principal ultrafilter on is the collection of all subsets of that contain a fixed element . The ultrafilters that are not principal are the free ultrafilters. The existence of free ultrafilters on any infinite set is implied by the ultrafilter lemma, which can be proven in ZFC. On the other hand, there exists models of ZF where every ultrafilter on a set is principal.
Ultrafilters have many applications in set theory, model theory, and topology.[1]: 186 Usually, only free ultrafilters lead to non-trivial constructions. For example, an ultraproduct modulo a principal ultrafilter is always isomorphic to one of the factors, while an ultraproduct modulo a free ultrafilter usually has a more complex structure.
Definitions
editGiven an arbitrary set an ultrafilter on is a non-empty family of subsets of such that:
- Proper or non-degenerate: The empty set is not an element of
- Upward closed in : If and if is any superset of (that is, if ) then
- π−system: If and are elements of then so is their intersection
- If then either or its complement is an element of [note 1]
Properties (1), (2), and (3) are the defining properties of a filter on Some authors do not include non-degeneracy (which is property (1) above) in their definition of "filter". However, the definition of "ultrafilter" (and also of "prefilter" and "filter subbase") always includes non-degeneracy as a defining condition. This article requires that all filters be proper although a filter might be described as "proper" for emphasis.
A filter subbase is a non-empty family of sets that has the finite intersection property (i.e. all finite intersections are non-empty). Equivalently, a filter subbase is a non-empty family of sets that is contained in some (proper) filter. The smallest (relative to ) filter containing a given filter subbase is said to be generated by the filter subbase.
The upward closure in of a family of sets is the set
A prefilter or filter base is a non-empty and proper (i.e. ) family of sets that is downward directed, which means that if then there exists some such that Equivalently, a prefilter is any family of sets whose upward closure is a filter, in which case this filter is called the filter generated by and is said to be a filter base for
The dual in [2] of a family of sets is the set For example, the dual of the power set is itself: A family of sets is a proper filter on if and only if its dual is a proper ideal on ("proper" means not equal to the power set).
Generalization to ultra prefilters
editA family of subsets of is called ultra if and any of the following equivalent conditions are satisfied:[2][3]
- For every set there exists some set such that or (or equivalently, such that equals or ).
- For every set there exists some set such that equals or
- Here, is defined to be the union of all sets in
- This characterization of " is ultra" does not depend on the set so mentioning the set is optional when using the term "ultra."
- For every set (not necessarily even a subset of ) there exists some set such that equals or
- If satisfies this condition then so does every superset In particular, a set is ultra if and only if and contains as a subset some ultra family of sets.
A filter subbase that is ultra is necessarily a prefilter.[proof 1]
The ultra property can now be used to define both ultrafilters and ultra prefilters:
- An ultra prefilter[2][3] is a prefilter that is ultra. Equivalently, it is a filter subbase that is ultra.
- An ultrafilter[2][3] on is a (proper) filter on that is ultra. Equivalently, it is any filter on that is generated by an ultra prefilter.
Ultra prefilters as maximal prefilters
To characterize ultra prefilters in terms of "maximality," the following relation is needed.
- Given two families of sets and the family is said to be coarser[4][5] than and is finer than and subordinate to written or N ⊢ M, if for every there is some such that The families and are called equivalent if and The families and are comparable if one of these sets is finer than the other.[4]
The subordination relationship, i.e. is a preorder so the above definition of "equivalent" does form an equivalence relation. If then but the converse does not hold in general. However, if is upward closed, such as a filter, then if and only if Every prefilter is equivalent to the filter that it generates. This shows that it is possible for filters to be equivalent to sets that are not filters.
If two families of sets and are equivalent then either both and are ultra (resp. prefilters, filter subbases) or otherwise neither one of them is ultra (resp. a prefilter, a filter subbase). In particular, if a filter subbase is not also a prefilter, then it is not equivalent to the filter or prefilter that it generates. If and are both filters on then and are equivalent if and only if If a proper filter (resp. ultrafilter) is equivalent to a family of sets then is necessarily a prefilter (resp. ultra prefilter). Using the following characterization, it is possible to define prefilters (resp. ultra prefilters) using only the concept of filters (resp. ultrafilters) and subordination:
- An arbitrary family of sets is a prefilter if and only it is equivalent to a (proper) filter.
- An arbitrary family of sets is an ultra prefilter if and only it is equivalent to an ultrafilter.
Characterizations
editThere are no ultrafilters on the empty set, so it is henceforth assumed that is nonempty.
A filter subbase on is an ultrafilter on if and only if any of the following equivalent conditions hold:[2][3]
- for any either or
- is a maximal filter subbase on meaning that if is any filter subbase on then implies [6]
A (proper) filter on is an ultrafilter on if and only if any of the following equivalent conditions hold:
- is ultra;
- is generated by an ultra prefilter;
- For any subset or [6]
- So an ultrafilter decides for every whether is "large" (i.e. ) or "small" (i.e. ).[7]
- For each subset either[note 1] is in or ( ) is.
- This condition can be restated as: is partitioned by and its dual
- The sets and are disjoint for all prefilters on
- is an ideal on [6]
- For any finite family of subsets of (where ), if then for some index
- In words, a "large" set cannot be a finite union of sets none of which is large.[8]
- For any if then or
- For any if then or (a filter with this property is called a prime filter).
- For any if and then either or
- is a maximal filter; that is, if is a filter on such that then Equivalently, is a maximal filter if there is no filter on that contains as a proper subset (that is, no filter is strictly finer than ).[6]
Grills and filter-grills
editIf then its grill on is the family where may be written if is clear from context. For example, and if then If then and moreover, if is a filter subbase then [9] The grill is upward closed in if and only if which will henceforth be assumed. Moreover, so that is upward closed in if and only if
The grill of a filter on is called a filter-grill on [9] For any is a filter-grill on if and only if (1) is upward closed in and (2) for all sets and if then or The grill operation induces a bijection
whose inverse is also given by [9] If then is a filter-grill on if and only if [9] or equivalently, if and only if is an ultrafilter on [9] That is, a filter on is a filter-grill if and only if it is ultra. For any non-empty is both a filter on and a filter-grill on if and only if (1) and (2) for all the following equivalences hold:
- if and only if if and only if [9]
Free or principal
editIf is any non-empty family of sets then the Kernel of is the intersection of all sets in [10]
A non-empty family of sets is called:
- free if and fixed otherwise (that is, if ).
- principal if
- principal at a point if and is a singleton set; in this case, if then is said to be principal at
If a family of sets is fixed then is ultra if and only if some element of is a singleton set, in which case will necessarily be a prefilter. Every principal prefilter is fixed, so a principal prefilter is ultra if and only if is a singleton set. A singleton set is ultra if and only if its sole element is also a singleton set.
The next theorem shows that every ultrafilter falls into one of two categories: either it is free or else it is a principal filter generated by a single point.
Proposition — If is an ultrafilter on then the following are equivalent:
- is fixed, or equivalently, not free.
- is principal.
- Some element of is a finite set.
- Some element of is a singleton set.
- is principal at some point of which means for some
- does not contain the Fréchet filter on as a subset.
- is sequential.[9]
Every filter on that is principal at a single point is an ultrafilter, and if in addition is finite, then there are no ultrafilters on other than these.[10] In particular, if a set has finite cardinality then there are exactly ultrafilters on and those are the ultrafilters generated by each singleton subset of Consequently, free ultrafilters can only exist on an infinite set.
Examples, properties, and sufficient conditions
editIf is an infinite set then there are as many ultrafilters over as there are families of subsets of explicitly, if has infinite cardinality then the set of ultrafilters over has the same cardinality as that cardinality being [11]
If and are families of sets such that is ultra, and then is necessarily ultra. A filter subbase that is not a prefilter cannot be ultra; but it is nevertheless still possible for the prefilter and filter generated by to be ultra.
Suppose is ultra and is a set. The trace is ultra if and only if it does not contain the empty set. Furthermore, at least one of the sets and will be ultra (this result extends to any finite partition of ). If are filters on is an ultrafilter on and then there is some that satisfies [12] This result is not necessarily true for an infinite family of filters.[12]
The image under a map of an ultra set is again ultra and if is an ultra prefilter then so is The property of being ultra is preserved under bijections. However, the preimage of an ultrafilter is not necessarily ultra, not even if the map is surjective. For example, if has more than one point and if the range of consists of a single point then is an ultra prefilter on but its preimage is not ultra. Alternatively, if is a principal filter generated by a point in then the preimage of contains the empty set and so is not ultra.
The elementary filter induced by an infinite sequence, all of whose points are distinct, is not an ultrafilter.[12] If then denotes the set consisting all subsets of having cardinality and if contains at least ( ) distinct points, then is ultra but it is not contained in any prefilter. This example generalizes to any integer and also to if contains more than one element. Ultra sets that are not also prefilters are rarely used.
For every and every let If is an ultrafilter on then the set of all such that is an ultrafilter on [13]
Monad structure
editThe functor associating to any set the set of of all ultrafilters on forms a monad called the ultrafilter monad. The unit map sends any element to the principal ultrafilter given by
This ultrafilter monad is the codensity monad of the inclusion of the category of finite sets into the category of all sets,[14] which gives a conceptual explanation of this monad.
Similarly, the ultraproduct monad is the codensity monad of the inclusion of the category of finite families of sets into the category of all families of set. So in this sense, ultraproducts are categorically inevitable.[14]
The ultrafilter lemma
editThe ultrafilter lemma was first proved by Alfred Tarski in 1930.[13]
The ultrafilter lemma/principle/theorem[4] — Every proper filter on a set is contained in some ultrafilter on
The ultrafilter lemma is equivalent to each of the following statements:
- For every prefilter on a set there exists a maximal prefilter on subordinate to it.[2]
- Every proper filter subbase on a set is contained in some ultrafilter on
A consequence of the ultrafilter lemma is that every filter is equal to the intersection of all ultrafilters containing it.[15][note 2]
The following results can be proven using the ultrafilter lemma. A free ultrafilter exists on a set if and only if is infinite. Every proper filter is equal to the intersection of all ultrafilters containing it.[4] Since there are filters that are not ultra, this shows that the intersection of a family of ultrafilters need not be ultra. A family of sets can be extended to a free ultrafilter if and only if the intersection of any finite family of elements of is infinite.
Relationships to other statements under ZF
editThroughout this section, ZF refers to Zermelo–Fraenkel set theory and ZFC refers to ZF with the Axiom of Choice (AC). The ultrafilter lemma is independent of ZF. That is, there exist models in which the axioms of ZF hold but the ultrafilter lemma does not. There also exist models of ZF in which every ultrafilter is necessarily principal.
Every filter that contains a singleton set is necessarily an ultrafilter and given the definition of the discrete ultrafilter does not require more than ZF. If is finite then every ultrafilter is a discrete filter at a point; consequently, free ultrafilters can only exist on infinite sets. In particular, if is finite then the ultrafilter lemma can be proven from the axioms ZF. The existence of free ultrafilter on infinite sets can be proven if the axiom of choice is assumed. More generally, the ultrafilter lemma can be proven by using the axiom of choice, which in brief states that any Cartesian product of non-empty sets is non-empty. Under ZF, the axiom of choice is, in particular, equivalent to (a) Zorn's lemma, (b) Tychonoff's theorem, (c) the weak form of the vector basis theorem (which states that every vector space has a basis), (d) the strong form of the vector basis theorem, and other statements. However, the ultrafilter lemma is strictly weaker than the axiom of choice. While free ultrafilters can be proven to exist, it is not possible to construct an explicit example of a free ultrafilter (using only ZF and the ultrafilter lemma); that is, free ultrafilters are intangible.[16] Alfred Tarski proved that under ZFC, the cardinality of the set of all free ultrafilters on an infinite set is equal to the cardinality of where denotes the power set of [17] Other authors attribute this discovery to Bedřich Pospíšil (following a combinatorial argument from Fichtenholz, and Kantorovitch, improved by Hausdorff).[18][19]
Under ZF, the axiom of choice can be used to prove both the ultrafilter lemma and the Krein–Milman theorem; conversely, under ZF, the ultrafilter lemma together with the Krein–Milman theorem can prove the axiom of choice.[20]
Statements that cannot be deduced
editThe ultrafilter lemma is a relatively weak axiom. For example, each of the statements in the following list can not be deduced from ZF together with only the ultrafilter lemma:
- A countable union of countable sets is a countable set.
- The axiom of countable choice (ACC).
- The axiom of dependent choice (ADC).
Equivalent statements
editUnder ZF, the ultrafilter lemma is equivalent to each of the following statements:[21]
- The Boolean prime ideal theorem (BPIT).
- Stone's representation theorem for Boolean algebras.
- Any product of Boolean spaces is a Boolean space.[22]
- Boolean Prime Ideal Existence Theorem: Every nondegenerate Boolean algebra has a prime ideal.[23]
- Tychonoff's theorem for Hausdorff spaces: Any product of compact Hausdorff spaces is compact.[22]
- If is endowed with the discrete topology then for any set the product space is compact.[22]
- Each of the following versions of the Banach-Alaoglu theorem is equivalent to the ultrafilter lemma:
- Any equicontinuous set of scalar-valued maps on a topological vector space (TVS) is relatively compact in the weak-* topology (that is, it is contained in some weak-* compact set).[24]
- The polar of any neighborhood of the origin in a TVS is a weak-* compact subset of its continuous dual space.[24]
- The closed unit ball in the continuous dual space of any normed space is weak-* compact.[24]
- If the normed space is separable then the ultrafilter lemma is sufficient but not necessary to prove this statement.
- A topological space is compact if every ultrafilter on converges to some limit.[25]
- A topological space is compact if and only if every ultrafilter on converges to some limit.[25]
- The addition of the words "and only if" is the only difference between this statement and the one immediately above it.
- The Alexander subbase theorem.[26][27]
- The Ultranet lemma: Every net has a universal subnet.[27]
- A topological space is compact if and only if every ultranet on converges to some limit.[25]
- If the words "and only if" are removed then the resulting statement remains equivalent to the ultrafilter lemma.[25]
- A convergence space is compact if every ultrafilter on converges.[25]
- A uniform space is compact if it is complete and totally bounded.[25]
- The Stone–Čech compactification Theorem.[22]
- Each of the following versions of the compactness theorem is equivalent to the ultrafilter lemma:
- If is a set of first-order sentences such that every finite subset of has a model, then has a model.[28]
- If is a set of zero-order sentences such that every finite subset of has a model, then has a model.[28]
- The completeness theorem: If is a set of zero-order sentences that is syntactically consistent, then it has a model (that is, it is semantically consistent).
Weaker statements
editAny statement that can be deduced from the ultrafilter lemma (together with ZF) is said to be weaker than the ultrafilter lemma. A weaker statement is said to be strictly weaker if under ZF, it is not equivalent to the ultrafilter lemma. Under ZF, the ultrafilter lemma implies each of the following statements:
- The Axiom of Choice for Finite sets (ACF): Given and a family of non-empty finite sets, their product is not empty.[27]
- A countable union of finite sets is a countable set.
- However, ZF with the ultrafilter lemma is too weak to prove that a countable union of countable sets is a countable set.
- The Hahn–Banach theorem.[27]
- In ZF, the Hahn–Banach theorem is strictly weaker than the ultrafilter lemma.
- The Banach–Tarski paradox.
- In fact, under ZF, the Banach–Tarski paradox can be deduced from the Hahn–Banach theorem,[29][30] which is strictly weaker than the Ultrafilter Lemma.
- Every set can be linearly ordered.
- Every field has a unique algebraic closure.
- Non-trivial ultraproducts exist.
- The weak ultrafilter theorem: A free ultrafilter exists on
- Under ZF, the weak ultrafilter theorem does not imply the ultrafilter lemma; that is, it is strictly weaker than the ultrafilter lemma.
- There exists a free ultrafilter on every infinite set;
- This statement is actually strictly weaker than the ultrafilter lemma.
- ZF alone does not even imply that there exists a non-principal ultrafilter on some set.
Completeness
editThe completeness of an ultrafilter on a powerset is the smallest cardinal κ such that there are κ elements of whose intersection is not in The definition of an ultrafilter implies that the completeness of any powerset ultrafilter is at least . An ultrafilter whose completeness is greater than —that is, the intersection of any countable collection of elements of is still in —is called countably complete or σ-complete.
The completeness of a countably complete nonprincipal ultrafilter on a powerset is always a measurable cardinal.[citation needed]
Ordering on ultrafilters
editThe Rudin–Keisler ordering (named after Mary Ellen Rudin and Howard Jerome Keisler) is a preorder on the class of powerset ultrafilters defined as follows: if is an ultrafilter on and an ultrafilter on then if there exists a function such that
- if and only if
for every subset
Ultrafilters and are called Rudin–Keisler equivalent, denoted U ≡RK V, if there exist sets and and a bijection that satisfies the condition above. (If and have the same cardinality, the definition can be simplified by fixing )
It is known that ≡RK is the kernel of ≤RK, i.e., that U ≡RK V if and only if and [31]
Ultrafilters on ℘(ω)
edit
There are several special properties that an ultrafilter on where extends the natural numbers, may possess, which prove useful in various areas of set theory and topology.
- A non-principal ultrafilter is called a P-point (or weakly selective) if for every partition of such that for all there exists some such that is a finite set for each
- A non-principal ultrafilter is called Ramsey (or selective) if for every partition of such that for all there exists some such that is a singleton set for each
It is a trivial observation that all Ramsey ultrafilters are P-points. Walter Rudin proved that the continuum hypothesis implies the existence of Ramsey ultrafilters.[32] In fact, many hypotheses imply the existence of Ramsey ultrafilters, including Martin's axiom. Saharon Shelah later showed that it is consistent that there are no P-point ultrafilters.[33] Therefore, the existence of these types of ultrafilters is independent of ZFC.
P-points are called as such because they are topological P-points in the usual topology of the space βω \ ω of non-principal ultrafilters. The name Ramsey comes from Ramsey's theorem. To see why, one can prove that an ultrafilter is Ramsey if and only if for every 2-coloring of there exists an element of the ultrafilter that has a homogeneous color.
An ultrafilter on is Ramsey if and only if it is minimal in the Rudin–Keisler ordering of non-principal powerset ultrafilters.[34]
See also
edit- Extender (set theory) – in set theory, a system of ultrafilters representing an elementary embedding witnessing large cardinal properties
- Filter (mathematics) – In mathematics, a special subset of a partially ordered set
- Filter (set theory) – Family of sets representing "large" sets
- Filters in topology – Use of filters to describe and characterize all basic topological notions and results.
- Łoś's theorem – Mathematical construction
- Ultrafilter – Maximal proper filter
- Universal net – A generalization of a sequence of points
Notes
edit- ^ a b Properties 1 and 3 imply that and cannot both be elements of
- ^ Let be a filter on that is not an ultrafilter. If is such that then has the finite intersection property (because if then if and only if ) so that by the ultrafilter lemma, there exists some ultrafilter on such that (so in particular ). It follows that
Proofs
- ^ Suppose is filter subbase that is ultra. Let and define Because is ultra, there exists some such that equals or The finite intersection property implies that so necessarily which is equivalent to
References
edit- ^ Davey, B. A.; Priestley, H. A. (1990). Introduction to Lattices and Order. Cambridge Mathematical Textbooks. Cambridge University Press.
- ^ a b c d e f g Narici & Beckenstein 2011, pp. 2–7.
- ^ a b c d e f g Dugundji 1966, pp. 219–221.
- ^ a b c d Bourbaki 1989, pp. 57–68.
- ^ Schubert 1968, pp. 48–71.
- ^ a b c d Schechter 1996, pp. 100–130.
- ^ Higgins, Cecelia (2018). "Ultrafilters in set theory" (PDF). math.uchicago.edu. Retrieved August 16, 2020.
- ^ Kruckman, Alex (November 7, 2012). "Notes on Ultrafilters" (PDF). math.berkeley.edu. Retrieved August 16, 2020.
- ^ a b c d e f g Dolecki & Mynard 2016, pp. 27–54.
- ^ a b Dolecki & Mynard 2016, pp. 33–35.
- ^ Pospíšil, Bedřich (1937). "Remark on Bicompact Spaces". The Annals of Mathematics. 38 (4): 845–846. doi:10.2307/1968840. JSTOR 1968840.
- ^ a b c Bourbaki 1989, pp. 129–133.
- ^ a b Jech 2006, pp. 73–89.
- ^ a b Leinster, Tom (2013). "Codensity and the ultrafilter monad" (PDF). Theory and Applications of Categories. 28: 332–370. arXiv:1209.3606. Bibcode:2012arXiv1209.3606L.
- ^ Bourbaki 1987, pp. 57–68.
- ^ Schechter 1996, p. 105.
- ^ Schechter 1996, pp. 150–152.
- ^ Jech 2006, pp. 75–76.
- ^ Comfort 1977, p. 420.
- ^ Bell, J.; Fremlin, David (1972). "A geometric form of the axiom of choice" (PDF). Fundamenta Mathematicae. 77 (2): 167–170. doi:10.4064/fm-77-2-167-170. Retrieved 11 June 2018.
Theorem 1.2. BPI [the Boolean Prime Ideal Theorem] & KM [Krein-Milman] (*) [the unit ball of the dual of a normed vector space has an extreme point].... Theorem 2.1. (*) AC [the Axiom of Choice].
- ^ Schechter 1996, pp. 105, 150–160, 166, 237, 317–315, 338–340, 344–346, 386–393, 401–402, 455–456, 463, 474, 506, 766–767.
- ^ a b c d Schechter 1996, p. 463.
- ^ Schechter 1996, p. 339.
- ^ a b c Schechter 1996, pp. 766–767.
- ^ a b c d e f Schechter 1996, p. 455.
- ^ Hodel, R.E. (2005). "Restricted versions of the Tukey-Teichmüller theorem that are equivalent to the Boolean prime ideal theorem". Archive for Mathematical Logic. 44 (4): 459–472. doi:10.1007/s00153-004-0264-9. S2CID 6507722.
- ^ a b c d Muger, Michael (2020). Topology for the Working Mathematician.
- ^ a b Schechter 1996, pp. 391–392.
- ^ Foreman, M.; Wehrung, F. (1991). "The Hahn–Banach theorem implies the existence of a non-Lebesgue measurable set" (PDF). Fundamenta Mathematicae. 138: 13–19. doi:10.4064/fm-138-1-13-19.
- ^ Pawlikowski, Janusz (1991). "The Hahn–Banach theorem implies the Banach–Tarski paradox" (PDF). Fundamenta Mathematicae. 138: 21–22. doi:10.4064/fm-138-1-21-22.
- ^ Comfort, W. W.; Negrepontis, S. (1974). The theory of ultrafilters. Berlin, New York: Springer-Verlag. MR 0396267. Corollary 9.3.
- ^ Rudin, Walter (1956), "Homogeneity problems in the theory of Čech compactifications", Duke Mathematical Journal, 23 (3): 409–419, doi:10.1215/S0012-7094-56-02337-7, hdl:10338.dmlcz/101493
- ^ Wimmers, Edward (March 1982), "The Shelah P-point independence theorem", Israel Journal of Mathematics, 43 (1): 28–48, doi:10.1007/BF02761683, S2CID 122393776
- ^ Jech 2006, p. 91(Left as exercise 7.12)
Bibliography
edit- Arkhangel'skii, Alexander Vladimirovich; Ponomarev, V.I. (1984). Fundamentals of General Topology: Problems and Exercises. Mathematics and Its Applications. Vol. 13. Dordrecht Boston: D. Reidel. ISBN 978-90-277-1355-1. OCLC 9944489.
- Bourbaki, Nicolas (1989) [1966]. General Topology: Chapters 1–4 [Topologie Générale]. Éléments de mathématique. Berlin New York: Springer Science & Business Media. ISBN 978-3-540-64241-1. OCLC 18588129.
- Dixmier, Jacques (1984). General Topology. Undergraduate Texts in Mathematics. Translated by Berberian, S. K. New York: Springer-Verlag. ISBN 978-0-387-90972-1. OCLC 10277303.
- Dolecki, Szymon; Mynard, Frédéric (2016). Convergence Foundations Of Topology. New Jersey: World Scientific Publishing Company. ISBN 978-981-4571-52-4. OCLC 945169917.
- Dugundji, James (1966). Topology. Boston: Allyn and Bacon. ISBN 978-0-697-06889-7. OCLC 395340485.
- Császár, Ákos (1978). General topology. Translated by Császár, Klára. Bristol England: Adam Hilger Ltd. ISBN 0-85274-275-4. OCLC 4146011.
- Jech, Thomas (2006). Set Theory: The Third Millennium Edition, Revised and Expanded. Berlin New York: Springer Science & Business Media. ISBN 978-3-540-44085-7. OCLC 50422939.
- Joshi, K. D. (1983). Introduction to General Topology. New York: John Wiley and Sons Ltd. ISBN 978-0-85226-444-7. OCLC 9218750.
- Narici, Lawrence; Beckenstein, Edward (2011). Topological Vector Spaces. Pure and applied mathematics (Second ed.). Boca Raton, FL: CRC Press. ISBN 978-1584888666. OCLC 144216834.
- Schechter, Eric (1996). Handbook of Analysis and Its Foundations. San Diego, CA: Academic Press. ISBN 978-0-12-622760-4. OCLC 175294365.
- Schubert, Horst (1968). Topology. London: Macdonald & Co. ISBN 978-0-356-02077-8. OCLC 463753.
Further reading
edit- Comfort, W. W. (1977). "Ultrafilters: some old and some new results" (PDF). Bulletin of the American Mathematical Society. 83 (4): 417–455. doi:10.1090/S0002-9904-1977-14316-4. ISSN 0002-9904. MR 0454893.
- Comfort, W. W.; Negrepontis, S. (1974), The theory of ultrafilters, Berlin, New York: Springer-Verlag, MR 0396267
- Ultrafilter at the nLab






