In the mathematical field of graph theory, the Chang graphs are three 12-regular undirected graphs, each with 28 vertices and 168 edges. They are strongly regular, with the same parameters and spectrum as the line graph L(K8) of the complete graph K8.
| Chang graphs | |
|---|---|
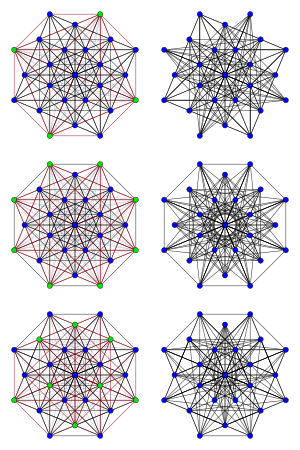 The three Chang graphs (right), and the switching sets generating them from the line graph L(K8) (green, left) | |
| Vertices | 28 |
| Edges | 168 |
| Radius | 2 |
| Diameter | 2 |
| Girth | 3 |
| Automorphisms | 96360384 |
| Properties | Strongly regular |
| Table of graphs and parameters | |
Each of these three graphs may be obtained by graph switching from L(K8). That is, a subset S of the vertices of L(K8) is chosen, each edge that connects a vertex in S with a vertex not in S is deleted from L(K8), and an edge is added for each pair of vertices (with again one in S and one not in S) that were not already connected by an edge. Among the graphs that can be generated in this way, three of them are the Chang graphs.
The Chang graphs are named after Chang Li-Chien, who proved that, with only these exceptions, every line graph of a complete graph is uniquely determined by its parameters as a strongly regular graph.[1]
See also
edit- Shrikhande graph, a similar exception to the uniqueness of the strongly regular graphs L(Kn,n)
References
edit- ^ Chang Li-Chien (1959), "The uniqueness and non-uniqueness of the triangular association schemes", Science Record (Peking), New. Ser., 3: 604–613.