Disphenocingulum

Disphenocingulum
Disphenocingulum
Type	Johnson; J89 – J90 – J91
Faces	20 triangles; 4 squares
Edges	38
Vertices	16
Vertex configuration	4(32.42) ; 4(35) ; 8(34.4)
Symmetry group	D2d
Properties	convex, elementary
Net

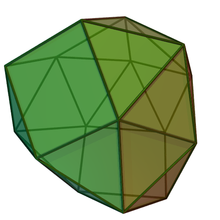
In geometry, the disphenocingulum is a Johnson solid with 20 equilateral triangles and 4 squares as its faces.

Properties

The disphenocingulum is named by Johnson (1966). The prefix dispheno- refers to two wedgelike complexes, each formed by two adjacent lunes—a figure of two equilateral triangles at the opposite sides of a square. The suffix -cingulum, literally 'belt', refers to a band of 12 triangles joining the two wedges.^[1] The resulting polyhedron has 20 equilateral triangles and 4 squares, making 24 faces.^[2]. All of the faces are regular, categorizing the disphenocingulum as a Johnson solid—a convex polyhedron in which all of its faces are regular polygon—enumerated as 90th Johnson solid $J_{90}$ .^[3]. It is an elementary polyhedron, meaning that it cannot be separated by a plane into two small regular-faced polyhedra.^[4]

The surface area of a disphenocingulum with edge length $a$ can be determined by adding all of its faces, the area of 20 equilateral triangles and 4 squares $(4+5{\sqrt {3}})a^{2}\approx 12.6603a^{2}$ , and its volume is $3.7776a^{3}$ .^[2]

Cartesian coordinates

Let $a\approx 0.76713$ be the second smallest positive root of the polynomial ${\begin{aligned}&256x^{12}-512x^{11}-1664x^{10}+3712x^{9}+1552x^{8}-6592x^{7}\\&\quad {}+1248x^{6}+4352x^{5}-2024x^{4}-944x^{3}+672x^{2}-24x-23\end{aligned}}$ and $h={\sqrt {2+8a-8a^{2}}}$ and $c={\sqrt {1-a^{2}}}$ . Then, the Cartesian coordinates of a disphenocingulum with edge length 2 are given by the union of the orbits of the points $\left(1,2a,{\frac {h}{2}}\right),\ \left(1,0,2c+{\frac {h}{2}}\right),\ \left(1+{\frac {\sqrt {3-4a^{2}}}{c}},0,2c-{\frac {1}{c}}+{\frac {h}{2}}\right)$ under the action of the group generated by reflections about the xz-plane and the yz-plane.^[5]

References

^ Johnson, N. W. (1966). "Convex polyhedra with regular faces". Canadian Journal of Mathematics. 18: 169–200. doi:10.4153/cjm-1966-021-8. MR 0185507. S2CID 122006114. Zbl 0132.14603.
^ ^a ^b Berman, M. (1971). "Regular-faced convex polyhedra". Journal of the Franklin Institute. 291 (5): 329–352. doi:10.1016/0016-0032(71)90071-8. MR 0290245.
^ Francis, D. (August 2013). "Johnson solids & their acronyms". Word Ways. 46 (3): 177.
^ Cromwell, P. R. (1997). Polyhedra. Cambridge University Press. p. 86–87, 89. ISBN 978-0-521-66405-9.
^ Timofeenko, A. V. (2009). "The non-Platonic and non-Archimedean noncomposite polyhedra". Journal of Mathematical Science. 162 (5): 717. doi:10.1007/s10958-009-9655-0. S2CID 120114341.

External links

Weisstein, Eric W., "Disphenocingulum" ("Johnson solid") at MathWorld.

[johnson-1] Johnson, N. W. (1966). "Convex polyhedra with regular faces". Canadian Journal of Mathematics. 18: 169–200. doi:10.4153/cjm-1966-021-8. MR 0185507. S2CID 122006114. Zbl 0132.14603.

[berman-2] Berman, M. (1971). "Regular-faced convex polyhedra". Journal of the Franklin Institute. 291 (5): 329–352. doi:10.1016/0016-0032(71)90071-8. MR 0290245.

[francis-3] Francis, D. (August 2013). "Johnson solids & their acronyms". Word Ways. 46 (3): 177.

[cromwell-4] Cromwell, P. R. (1997). Polyhedra. Cambridge University Press. p. 86–87, 89. ISBN 978-0-521-66405-9.

[timofeenko-5] Timofeenko, A. V. (2009). "The non-Platonic and non-Archimedean noncomposite polyhedra". Journal of Mathematical Science. 162 (5): 717. doi:10.1007/s10958-009-9655-0. S2CID 120114341.

[1]

[2]

[3]

[4]

[5]

Disphenocingulum

Type	Johnson $J 89 - J 90 - J 91$
Faces	20 triangles 4 squares
Edges	38
Vertices	16
Vertex configuration	$4(3 2 .4 2) 4(3 5) 8(3 4 .4)$
Symmetry group	$D 2d$
Properties	convex, elementary
Net