Dodecadodecahedron

Dodecadodecahedron
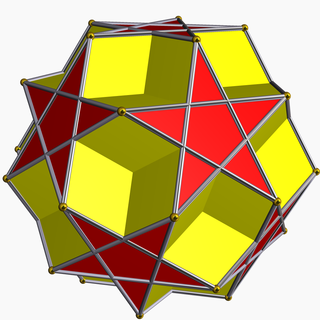
Type	Uniform star polyhedron
Elements	F = 24, E = 60 V = 30 (χ = −6)
Faces by sides	12{5}+12{5/2}
Coxeter diagram
Wythoff symbol	2 | 5 5/2 2 | 5 5/3 2 | 5/2 5/4 2 | 5/3 5/4
Symmetry group	Ih, [5,3], *532
Index references	U36, C45, W73
Dual polyhedron	Medial rhombic triacontahedron
Vertex figure	5.5/2.5.5/2
Bowers acronym	Did

In geometry, the dodecadodecahedron is a nonconvex uniform polyhedron, indexed as U₃₆. It is the rectification of the great dodecahedron (and that of its dual, the small stellated dodecahedron). It was discovered independently by Hess (1878), Badoureau (1881) and Pitsch (1882).

3D model of a dodecadodecahedron

The edges of this model form 10 central hexagons, and these, projected onto a sphere, become 10 great circles. These 10, along with the great circles from projections of two other polyhedra, form the 31 great circles of the spherical icosahedron used in construction of geodesic domes.

Wythoff constructions

It has four Wythoff constructions between four Schwarz triangle families: 2 | 5 5/2, 2 | 5 5/3, 2 | 5/2 5/4, 2 | 5/3 5/4, but represent identical results. Similarly it can be given four extended Schläfli symbols: r{5/2,5}, r{5/3,5}, r{5/2,5/4}, and r{5/3,5/4} or as Coxeter-Dynkin diagrams: , , , and .

Net

A shape with the same exterior appearance as the dodecadodecahedron can be constructed by folding up these nets:

12 pentagrams and 20 rhombic clusters are necessary. However, this construction replaces the crossing pentagonal faces of the dodecadodecahedron with non-crossing sets of rhombi, so it does not produce the same internal structure.

Related polyhedra

Its convex hull is the icosidodecahedron. It also shares its edge arrangement with the small dodecahemicosahedron (having the pentagrammic faces in common), and with the great dodecahemicosahedron (having the pentagonal faces in common).

Dodecadodecahedron	Small dodecahemicosahedron
Great dodecahemicosahedron	Icosidodecahedron (convex hull)

Animated truncation sequence from {5/2, 5} to {5, 5/2}

This polyhedron can be considered a rectified great dodecahedron. It is center of a truncation sequence between a small stellated dodecahedron and great dodecahedron:

The truncated small stellated dodecahedron looks like a dodecahedron on the surface, but it has 24 faces: 12 pentagons from the truncated vertices and 12 overlapping as (truncated pentagrams). The truncation of the dodecadodecahedron itself is not uniform and attempting to make it uniform results in a degenerate polyhedron (that looks like a small rhombidodecahedron with {10/2} polygons filling up the dodecahedral set of holes), but it has a uniform quasitruncation, the truncated dodecadodecahedron.

Name	Small stellated dodecahedron	Truncated small stellated dodecahedron	Dodecadodecahedron	Truncated great dodecahedron	Great dodecahedron
Coxeter-Dynkin diagram
Picture

It is topologically equivalent to a quotient space of the hyperbolic order-4 pentagonal tiling, by distorting the pentagrams back into regular pentagons. As such, it is topologically a regular polyhedron of index two:

Graphs of the dodecadodecahedron (left) and its dual (right) drawn in Bring's curve. The former is a quotient of the order-4 pentagonal and the latter of the order-5 square tiling. The letters (and colors) indicate, which sides of the fundamental 20-gon belong together. Faces cut by these sides are marked by colors.
24 pentagons 11 are complete, 10 are cut in half, 2 are cut in five pieces, 1 is cut in ten pieces	30 squares 20 are complete, 10 are cut in half

Medial rhombic triacontahedron

Medial rhombic triacontahedron
Type	Star polyhedron
Face
Elements	F = 30, E = 60 V = 24 (χ = −6)
Symmetry group	Ih, [5,3], *532
Index references	DU36
dual polyhedron	Dodecadodecahedron

The medial rhombic triacontahedron is the dual of the dodecadodecahedron. It has 30 intersecting rhombic faces.

Related hyperbolic tiling

It is topologically equivalent to a quotient space of the hyperbolic order-5 square tiling, by distorting the rhombi into squares. As such, it is topologically a regular polyhedron of index two:

Note that the order-5 square tiling is dual to the order-4 pentagonal tiling, and a quotient space of the order-4 pentagonal tiling is topologically equivalent to the dual of the medial rhombic triacontahedron, the dodecadodecahedron.

See also

• List of uniform polyhedra

References

• Badoureau (1881), "Mémoire sur les figures isoscèles", Journal de l'École Polytechnique, 49: 47–172
• Hess, Edmund (1878), Vier archimedeische Polyeder höherer Art, Cassel. Th. Kay, JFM 10.0346.03
• Pitsch (1882), "Über halbreguläre Sternpolyheder", Zeitschrift für das Realschulwesen, 7, JFM 14.0448.01
• Wenninger, Magnus (1983), Dual Models, Cambridge University Press, doi:10.1017/CBO9780511569371, ISBN 978-0-521-54325-5, MR 0730208

External links

• Weisstein, Eric W. "Dodecadodecahedron". MathWorld.
• Weisstein, Eric W. "Medial Rhombic Triacontahedron". MathWorld.
• Uniform polyhedra and duals