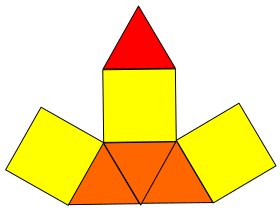
In geometry, the elongated triangular pyramid is one of the Johnson solids (J7). As the name suggests, it can be constructed by elongating a tetrahedron by attaching a triangular prism to its base. Like any elongated pyramid, the resulting solid is topologically (but not geometrically) self-dual.
| Elongated triangular pyramid | |
|---|---|
 | |
| Type | Johnson J6 – J7 – J8 |
| Faces | 4 triangles 3 squares |
| Edges | 12 |
| Vertices | 7 |
| Vertex configuration | 1(33) 3(3.42) 3(32.42) |
| Symmetry group | C3v, [3], (*33) |
| Rotation group | C3, [3]+, (33) |
| Dual polyhedron | self |
| Properties | convex |
| Net | |
 | |

Construction
editThe elongated triangular pyramid is constructed from a triangular prism by attaching regular tetrahedron onto one of its bases, a process known as elongation.[1] The tetrahedron covers an equilateral triangle, replacing it with three other equilateral triangles, so that the resulting polyhedron has four equilateral triangles and three squares as its faces.[2] A convex polyhedron in which all of the faces are regular polygons is called the Johnson solid, and the elongated triangular pyramid is among them, enumerated as the seventh Johnson solid .[3]
Properties
editAn elongated triangular pyramid with edge length has a height, by adding the height of a regular tetrahedron and a triangular prism:[4] Its surface area can be calculated by adding the area of all eight equilateral triangles and three squares:[2] and its volume can be calculated by slicing it into a regular tetrahedron and a prism, adding their volume up:[2]:
It has the three-dimensional symmetry group, the cyclic group of order 6. Its dihedral angle can be calculated by adding the angle of the tetrahedron and the triangular prism:[5]
- the dihedral angle of a tetrahedron between two adjacent triangular faces is ;
- the dihedral angle of the triangular prism between the square to its bases is , and the dihedral angle between square-to-triangle, on the edge where tetrahedron and triangular prism are attached, is ;
- the dihedral angle of the triangular prism between two adjacent square faces is the internal angle of an equilateral triangle .
References
edit- ^ Rajwade, A. R. (2001). Convex Polyhedra with Regularity Conditions and Hilbert's Third Problem. Texts and Readings in Mathematics. Hindustan Book Agency. p. 84–89. doi:10.1007/978-93-86279-06-4. ISBN 978-93-86279-06-4.
- ^ a b c Berman, Martin (1971). "Regular-faced convex polyhedra". Journal of the Franklin Institute. 291 (5): 329–352. doi:10.1016/0016-0032(71)90071-8. MR 0290245.
- ^ Uehara, Ryuhei (2020). Introduction to Computational Origami: The World of New Computational Geometry. Springer. p. 62. doi:10.1007/978-981-15-4470-5. ISBN 978-981-15-4470-5. S2CID 220150682.
- ^ Sapiña, R. "Area and volume of the Johnson solid ". Problemas y Ecuaciones (in Spanish). ISSN 2659-9899. Retrieved 2020-09-09.
- ^ Johnson, Norman W. (1966). "Convex polyhedra with regular faces". Canadian Journal of Mathematics. 18: 169–200. doi:10.4153/cjm-1966-021-8. MR 0185507. S2CID 122006114. Zbl 0132.14603.