Wikipedia

Solar cycle

(Redirected from Hale cycle)
This article is about the sunspot cycle. For the 28-year cycle of the calendar, see Solar cycle (calendar).

The solar cycle, also known as the solar magnetic activity cycle, sunspot cycle, or Schwabe cycle, is a nearly periodic 11-year change in the Sun's activity measured in terms of variations in the number of observed sunspots on the Sun's surface. Over the period of a solar cycle, levels of solar radiation and ejection of solar material, the number and size of sunspots, solar flares, and coronal loops all exhibit a synchronized fluctuation from a period of minimum activity to a period of a maximum activity back to a period of minimum activity.

Line graph showing historical sunspot number count, Maunder and Dalton minima, and the Modern Maximum
400 year sunspot history, including the Maunder Minimum
"The prediction for solar cycle 24 gave a smoothed sunspot number maximum of about 69 in the late Summer of 2013. The smoothed sunspot number reached 68.9 in August 2013 so the official maximum was at least that high. The smoothed sunspot number rose again towards this second peak over the last five months of 2016 and surpassed the level of the first peak (66.9 in February 2012). Many cycles are double peaked but this is the first in which the second peak in sunspot number was larger than the first. This was over five years into cycle 24. The predicted and observed size made this the smallest sunspot cycle since cycle 14 which had a maximum of 64.2 in February of 1906."[1]

The magnetic field of the Sun flips during each solar cycle, with the flip occurring when the solar cycle is near its maximum. After two solar cycles, the Sun's magnetic field returns to its original state, completing what is known as a Hale cycle.

This cycle has been observed for centuries by changes in the Sun's appearance and by terrestrial phenomena such as aurora but was not clearly identified until 1843. Solar activity, driven by both the solar cycle and transient aperiodic processes, governs the environment of interplanetary space by creating space weather and impacting space- and ground-based technologies as well as the Earth's atmosphere and also possibly climate fluctuations on scales of centuries and longer.

Understanding and predicting the solar cycle remains one of the grand challenges in astrophysics with major ramifications for space science and the understanding of magnetohydrodynamic phenomena elsewhere in the universe.

The current scientific consensus on climate change is that solar variations only play a marginal role in driving global climate change,[2] since the measured magnitude of recent solar variation is much smaller than the forcing due to greenhouse gases.[3]

Evolution of magnetism on the Sun

Definition

edit

Solar cycles have an average duration of about 11 years. Solar maximum and solar minimum refer to periods of maximum and minimum sunspot counts. Cycles span from one minimum to the next.

Observational history

edit
Main article: Solar observation
 
Samuel Heinrich Schwabe (1789–1875), German astronomer, discovered the solar cycle through extended observations of sunspots.
 
Rudolf Wolf (1816–1893), Swiss astronomer, carried out historical reconstruction of solar activity back to the 17th century.

The idea of a cyclical solar cycle was first hypothesized by Christian Horrebow based on his regular observations of sunspots made between 1761 and 1776 from the Rundetaarn observatory in Copenhagen, Denmark. In 1775, Horrebow noted how "it appears that after the course of a certain number of years, the appearance of the Sun repeats itself with respect to the number and size of the spots".[4] The solar cycle however would not be clearly identified until 1843 when Samuel Heinrich Schwabe noticed a periodic variation in the average number of sunspots after 17 years of solar observations.[5] Schwabe continued to observe the sunspot cycle for another 23 years, until 1867. In 1852, Rudolf Wolf designated the first numbered solar cycle to have started in February 1755 based on Schwabe's and other observations.[6] Wolf also created a standard sunspot number index, the Wolf number, which continues to be used today.

Between 1645 and 1715, very few sunspots were observed and recorded. This was first noted by Gustav Spörer and was later named the Maunder minimum after the wife-and-husband team Annie S. D. Maunder and Edward Walter Maunder who extensively researched this peculiar interval.[7]

In the second half of the nineteenth century Richard Carrington and Spörer independently noted the phenomena of sunspots appearing at different heliographic latitudes at different parts of the cycle. (See Spörer's law.) Alfred Harrison Joy would later describe how the magnitude at which the sunspots are "tilted"—with the leading spot(s) closer to the equator than the trailing spot(s)―grows with the latitude of these regions. (See Joy's law.)

The cycle's physical basis was elucidated by George Ellery Hale and collaborators, who in 1908 showed that sunspots were strongly magnetized (the first detection of magnetic fields beyond the Earth). In 1919 they identified a number of patterns that would collectively become known as Hale's law:

  • In the same heliographic hemisphere, bipolar active regions tend to have the same leading polarity.
  • In the opposite hemisphere (that is, on the other side of the solar equator) these regions tend to have the opposite leading polarity.
  • Leading polarities in both hemispheres flip from one sunspot cycle to the next.

Hale's observations revealed that the complete magnetic cycle—which would later be referred to as a Hale cycle—spans two solar cycles, or 22 years, before returning to its original state (including polarity). Because nearly all manifestations are insensitive to polarity, the 11-year solar cycle remains the focus of research; however, the two halves of the Hale cycle are typically not identical: the 11-year cycles usually alternate between higher and lower sums of Wolf's sunspot numbers (the Gnevyshev-Ohl rule).[8]

In 1961 the father-and-son team of Harold and Horace Babcock established that the solar cycle is a spatiotemporal magnetic process unfolding over the Sun as a whole. They observed that the solar surface is magnetized outside of sunspots, that this (weaker) magnetic field is to first order a dipole, and that this dipole undergoes polarity reversals with the same period as the sunspot cycle. Horace's Babcock Model described the Sun's oscillatory magnetic field as having a quasi-steady periodicity of 22 years.[5][9] It covered the oscillatory exchange of energy between toroidal and poloidal solar magnetic field components.

Cycle history

edit
 
Reconstruction of solar activity over 11,400 years

Sunspot numbers over the past 11,400 years have been reconstructed using carbon-14 and beryllium-10 isotope ratios.[10] The level of solar activity beginning in the 1940s is exceptional – the last period of similar magnitude occurred around 9,000 years ago (during the warm Boreal period).[11][12][13] The Sun was at a similarly high level of magnetic activity for only ~10% of the past 11,400 years. Almost all earlier high-activity periods were shorter than the present episode.[12] Fossil records suggest that the solar cycle has been stable for at least the last 700 million years. For example, the cycle length during the Early Permian is estimated to be 10.62 years[14] and similarly in the Neoproterozoic.[15][16]

 
Solar activity events recorded in radiocarbon. Present period is on right. Values since 1900 not shown.
Major events and approximate dates
Event Start End
Homeric minimum[17] 750 BCE 550 BCE
Oort minimum 1040 CE 1080 CE
Medieval maximum 1100 1250
Wolf minimum 1280 1350
Spörer Minimum 1450 1550
Maunder Minimum 1645 1715
Dalton Minimum 1790 1820
Modern Maximum 1933 2008

Until 2009, it was thought that 28 cycles had spanned the 309 years between 1699 and 2008, giving an average length of 11.04 years, but research then showed that the longest of these (1784–1799) may actually have been two cycles.[18][19] If so then the average length would be only around 10.7 years. Since observations began cycles as short as 9 years and as long as 14 years have been observed, and if the cycle of 1784–1799 is double then one of the two component cycles had to be less than 8 years in length. Significant amplitude variations also occur.

Several lists of proposed historical "grand minima" of solar activity exist.[11][20]

Recent cycles

edit

Cycle 25

edit
Main article: Solar cycle 25

Solar cycle 25 began in December 2019.[21] Several predictions have been made for solar cycle 25[22] based on different methods, ranging from very weak to strong magnitude. A physics-based prediction relying on the data-driven solar dynamo and solar surface flux transport models seems to have predicted the strength of the solar polar field at the current minima correctly and forecasts a weak but not insignificant solar cycle 25 similar to or slightly stronger than cycle 24.[23] Notably, they rule out the possibility of the Sun falling into a Maunder-minimum-like (inactive) state over the next decade. A preliminary consensus by a solar cycle 25 Prediction Panel was made in early 2019.[24] The Panel, which was organized by NOAA's Space Weather Prediction Center (SWPC) and NASA, based on the published solar cycle 25 predictions, concluded that solar cycle 25 will be very similar to solar cycle 24. They anticipate that the solar cycle minimum before cycle 25 will be long and deep, just as the minimum that preceded cycle 24. They expect solar maximum to occur between 2023 and 2026 with a sunspot range of 95 to 130, given in terms of the revised sunspot number.

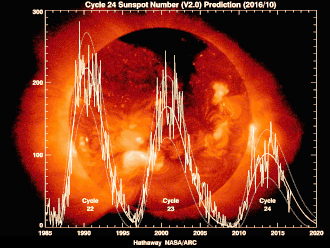
Cycle 24

edit
Main article: Solar cycle 24

Solar cycle 24 began on 4 January 2008,[25] with minimal activity until early 2010.[26][27] The cycle featured a "double-peaked" solar maximum. The first peak reached 99 in 2011 and the second in early 2014 at 101.[28] Cycle 24 ended in December 2019 after 11.0 years.[21]

Cycle 23

edit
Main article: Solar cycle 23

Solar cycle 23 lasted 11.6 years, beginning in May 1996 and ending in January 2008. The maximum smoothed sunspot number (monthly number of sunspots averaged over a twelve-month period) observed during the solar cycle was 120.8 (March 2000), and the minimum was 1.7.[29] A total of 805 days had no sunspots during this cycle.[30][31][32]

Phenomena

edit
Main article: Solar phenomena

Because the solar cycle reflects magnetic activity, various magnetically driven solar phenomena follow the solar cycle, including sunspots, faculae/plage, network, and coronal mass ejections.

Sunspots

edit
Main article: Sunspot
 
A drawing of a sunspot in the Chronicles of John of Worcester, ca. 1100[33]

The Sun's apparent surface, the photosphere, radiates more actively when there are more sunspots. Satellite monitoring of solar luminosity revealed a direct relationship between the solar cycle and luminosity with a peak-to-peak amplitude of about 0.1%.[34] Luminosity decreases by as much as 0.3% on a 10-day timescale when large groups of sunspots rotate across the Earth's view and increase by as much as 0.05% for up to 6 months due to faculae associated with large sunspot groups.[35]

The best information today comes from SOHO (a cooperative project of the European Space Agency and NASA), such as the MDI magnetogram, where the solar "surface" magnetic field can be seen.

As each cycle begins, sunspots appear at mid-latitudes, and then move closer and closer to the equator until a solar minimum is reached. This pattern is best visualized in the form of the so-called butterfly diagram. Images of the Sun are divided into latitudinal strips, and the monthly-averaged fractional surface of sunspots is calculated. This is plotted vertically as a color-coded bar, and the process is repeated month after month to produce this time-series diagram.

 
This version of the sunspot butterfly diagram was constructed by the solar group at NASA Marshall Space Flight Center. The newest version can be found at [http://solarcyclescience.com/solarcycle.html solarcyclescience.com

While magnetic field changes are concentrated at sunspots, the entire sun undergoes analogous changes, albeit of smaller magnitude.

 
Time vs. solar latitude diagram of the radial component of the solar magnetic field, averaged over successive solar rotation. The "butterfly" signature of sunspots is clearly visible at low latitudes. Diagram constructed by the solar group at NASA Marshall Space Flight Center. The newest version can be found at [http://solarcyclescience.com/solarcycle.html solarcyclescience.com

Faculae and plage

edit
Main articles: Solar facula and Solar plage
 
Solar plage area evolution over time

Faculae are bright magnetic features on the photosphere. They extend into the chromosphere, where they are referred to as plage. The evolution of plage areas is typically tracked from solar observations in the Ca II K line (393.37 nm).[36] The amount of facula and plage area varies in phase with the solar cycle, and they are more abundant than sunspots by approximately an order of magnitude.[37] They exhibit a non linear relation to sunspots.[38] Plage regions are also associated with strong magnetic fields in the solar surface.[39][40]

Solar flares and coronal mass ejections

edit
Main articles: Solar flare and Coronal mass ejection

The solar magnetic field structures the corona, giving it its characteristic shape visible at times of solar eclipses. Complex coronal magnetic field structures evolve in response to fluid motions at the solar surface, and emergence of magnetic flux produced by dynamo action in the solar interior. For reasons not yet understood in detail, sometimes these structures lose stability, leading to solar flares and coronal mass ejections (CME). Flares consist of an abrupt emission of energy (primarily at ultraviolet and X-ray wavelengths), which may or may not be accompanied by a coronal mass ejection, which consists of injection of energetic particles (primarily ionized hydrogen) into interplanetary space. Flares and CME are caused by sudden localized release of magnetic energy, which drives emission of ultraviolet and X-ray radiation as well as energetic particles. These eruptive phenomena can have a significant impact on Earth's upper atmosphere and space environment, and are the primary drivers of what is now called space weather. Consequently, the occurrence of both geomagnetic storms[41] and solar energetic particle[42] events shows a strong solar cycle variation, peaking close to sunspot maximum.

The occurrence frequency of coronal mass ejections and flares is strongly modulated by the cycle. Flares of any given size are some 50 times more frequent at solar maximum than at minimum. Large coronal mass ejections occur on average a few times a day at solar maximum, down to one every few days at solar minimum. The size of these events themselves does not depend sensitively on the phase of the solar cycle. A case in point are the three large X-class flares that occurred in December 2006, very near solar minimum; an X9.0 flare on Dec 5 stands as one of the brightest on record.[43]

Patterns

edit
 
An overview of three solar cycles shows the relationship between the solar cycle, galactic cosmic rays, and the state of Earth's near-space environment.[44]

Along with the approximately 11-year sunspot cycle, a number of additional patterns and cycles have been hypothesized.[8]

Waldmeier effect

edit

The Waldmeier effect describes the observation that the maximum amplitudes of solar cycles are inversely proportional to the time between their solar minima and maxima. Therefore, cycles with larger maximum amplitudes tend to take less time to reach their maxima than cycles with smaller amplitudes.[45] This effect was named after Max Waldmeier who first described it.[46]

Gnevyshev–Ohl rule

edit
Main article: Gnevyshev–Ohl rule

The Gnevyshev–Ohl rule describes the tendency for the sum of the Wolf number over an odd solar cycle to exceed that of the preceding even cycle.[8]

Gleissberg cycle

edit

The Gleissberg cycle describes an amplitude modulation of solar cycles with a period of about 70–100 years, or seven or eight solar cycles. It was named after Wolfgang Gleißberg.[8][47][48][49]

As pioneered by Ilya G. Usoskin and Sami Solanki, associated centennial variations in magnetic fields in the corona and heliosphere have been detected using carbon-14 and beryllium-10 cosmogenic isotopes stored in terrestrial reservoirs such as ice sheets and tree rings[50] and by using historic observations of geomagnetic storm activity, which bridge the time gap between the end of the usable cosmogenic isotope data and the start of modern satellite data.[51]

These variations have been successfully reproduced using models that employ magnetic flux continuity equations and observed sunspot numbers to quantify the emergence of magnetic flux from the top of the solar atmosphere and into the heliosphere,[52] showing that sunspot observations, geomagnetic activity and cosmogenic isotopes offer a convergent understanding of solar activity variations.

Suess cycle

edit

The Suess cycle, or de Vries cycle, is a cycle present in radiocarbon proxies of solar activity with a period of about 210 years. It was named after Hans Eduard Suess and Hessel de Vries.[48] Despite calculated radioisotope production rates being well correlated with the 400-year sunspot record, there is little evidence of the Suess cycle in the 400-year sunspot record by itself.[8]

Other hypothesized cycles

edit
 
2,300 year Hallstatt solar variation cycles

Periodicity of solar activity with periods longer than the solar cycle of about 11 (22) years has been proposed, including:

  • The Hallstatt cycle (named after a cool and wet period in Europe when glaciers advanced) is hypothesized to extend for approximately 2,400 years.[53][54][55][56]
  • In studies of carbon-14 ratios, cycles of 105, 131, 232, 385, 504, 805 and 2,241 years have been proposed, possibly matching cycles derived from other sources.[57] Damon and Sonett[58] proposed carbon 14-based medium- and short-term variations of periods 208 and 88 years; as well as suggesting a 2300-year radiocarbon period that modulates the 208-year period.[59]
  • Brückner-Egeson-Lockyer cycle (30 to 40 year cycles).
  • A 2021 study investigates the changes of the Pleistocene climate over the last 800 kyr from European Project for Ice Coring in Antarctica (EPICA) temperature (δD) and CO2-CH4 records[60] by using the benefits of the full-resolution methodology for time-series decomposition singular spectrum analysis, with a special focus on millennial-scale Sun-related signals.[61] The quantitative impact of the three Sun-related cycles (unnamed ~9.7-kyr; proposed 'Heinrich-Bond' ~6.0-kyr; Hallstatt ~2.5-kyr), cumulatively explain ~4.0% (δD), 2.9% (CO2), and 6.6% (CH4) in variance. A cycle of ~3.6 kyr, which is little known in literature, results in a mean variance of 0.6% only, does not seem to be Sun-related, although a gravitational origin cannot be ruled out. These 800-kyr-long EPICA suborbital records, which include millennial-scale Sun-related signals, fill an important gap in the field of solar cycles demonstrating for the first time the minor role of solar activity in the regional budget of Earth's climate system during the Mid-Late Pleistocene.

Effects

edit

Sun

edit
 
Activity cycles 21, 22 and 23 seen in sunspot number index, TSI, 10.7cm radio flux, and flare index. The vertical scales for each quantity have been adjusted to permit overplotting on the same vertical axis as TSI. Temporal variations of all quantities are tightly locked in phase, but the degree of correlation in amplitudes is variable to some degree.

Surface magnetism

edit

Sunspots eventually decay, releasing magnetic flux in the photosphere. This flux is dispersed and churned by turbulent convection and solar large-scale flows. These transport mechanisms lead to the accumulation of magnetized decay products at high solar latitudes, eventually reversing the polarity of the polar fields (notice how the blue and yellow fields reverse in the Hathaway/NASA/MSFC graph above).

The dipolar component of the solar magnetic field reverses polarity around the time of solar maximum and reaches peak strength at the solar minimum.

Space

edit

Spacecraft

edit

CMEs (coronal mass ejections) produce a radiation flux of high-energy protons, sometimes known as solar cosmic rays. These can cause radiation damage to electronics and solar cells in satellites. Solar proton events also can cause single-event upset (SEU) events on electronics; at the same, the reduced flux of galactic cosmic radiation during solar maximum decreases the high-energy component of particle flux.

CME radiation is dangerous to astronauts on a space mission who are outside the shielding produced by the Earth's magnetic field. Future mission designs (e.g., for a Mars Mission) therefore incorporate a radiation-shielded "storm shelter" for astronauts to retreat to during such an event.

Gleißberg developed a CME forecasting method that relies on consecutive cycles.[62]

The increased irradiance during solar maximum expands the envelope of the Earth's atmosphere, causing low-orbiting space debris to re-enter more quickly.

Galactic cosmic ray flux

edit

The outward expansion of solar ejecta into interplanetary space provides overdensities of plasma that are efficient at scattering high-energy cosmic rays entering the solar system from elsewhere in the galaxy. The frequency of solar eruptive events is modulated by the cycle, changing the degree of cosmic ray scattering in the outer solar system accordingly. As a consequence, the cosmic ray flux in the inner Solar System is anticorrelated with the overall level of solar activity.[63] This anticorrelation is clearly detected in cosmic ray flux measurements at the Earth's surface.

Some high-energy cosmic rays entering Earth's atmosphere collide hard enough with molecular atmospheric constituents that they occasionally cause nuclear spallation reactions. Fission products include radionuclides such as 14C and 10Be that settle on the Earth's surface. Their concentration can be measured in tree trunks or ice cores, allowing a reconstruction of solar activity levels into the distant past.[64] Such reconstructions indicate that the overall level of solar activity since the middle of the twentieth century stands amongst the highest of the past 10,000 years, and that epochs of suppressed activity, of varying durations have occurred repeatedly over that time span.[citation needed]

Atmospheric

edit

Solar irradiance

edit
Main article: Solar irradiance

The total solar irradiance (TSI) is the amount of solar radiative energy incident on the Earth's upper atmosphere. TSI variations were undetectable until satellite observations began in late 1978. A series of radiometers were launched on satellites since the 1970s.[65] TSI measurements varied from 1355 to 1375 W/m2 across more than ten satellites. One of the satellites, the ACRIMSAT was launched by the ACRIM group. The controversial 1989–1991 "ACRIM gap" between non-overlapping ACRIM satellites was interpolated by the ACRIM group into a composite showing +0.037%/decade rise. Another series based on the ACRIM data is produced by the PMOD group and shows a −0.008%/decade downward trend.[66] This 0.045%/decade difference can impact climate models. However, reconstructed total solar irradiance with models favor the PMOD series, thus reconciling the ACRIM-gap issue.[67][68]

Solar irradiance varies systematically over the cycle,[69] both in total irradiance and in its relative components (UV vs visible and other frequencies). The solar luminosity is an estimated 0.07 percent brighter during the mid-cycle solar maximum than the terminal solar minimum. Photospheric magnetism appears to be the primary cause (96%) of 1996–2013 TSI variation.[70] The ratio of ultraviolet to visible light varies.[71]

TSI varies in phase with the solar magnetic activity cycle[72] with an amplitude of about 0.1% around an average value of about 1361.5 W/m2[73] (the "solar constant"). Variations about the average of up to −0.3% are caused by large sunspot groups and of +0.05% by large faculae and the bright network on a 7-10-day timescale[74][75] Satellite-era TSI variations show small but detectable trends.[76][77]

TSI is higher at solar maximum, even though sunspots are darker (cooler) than the average photosphere. This is caused by magnetized structures other than sunspots during solar maxima, such as faculae and active elements of the "bright" network, that are brighter (hotter) than the average photosphere. They collectively overcompensate for the irradiance deficit associated with the cooler, but less numerous sunspots.[78] The primary driver of TSI changes on solar rotational and solar cycle timescales is the varying photospheric coverage of these radiatively active solar magnetic structures.[79]

Energy changes in UV irradiance involved in production and loss of ozone have atmospheric effects. The 30 hPa atmospheric pressure level changed height in phase with solar activity during solar cycles 20–23. UV irradiance increase caused higher ozone production, leading to stratospheric heating and to poleward displacements in the stratospheric and tropospheric wind systems.[80]

Short-wavelength radiation

edit
 
A solar cycle: a montage of ten years' worth of Yohkoh SXT images, demonstrating the variation in solar activity during a solar cycle, from after August 30, 1991, to September 6, 2001. Credit: the Yohkoh mission of ISAS (Japan) and NASA (US).

With a temperature of 5870 K, the photosphere emits a proportion of radiation in the extreme ultraviolet (EUV) and above. However, hotter upper layers of the Sun's atmosphere (chromosphere and corona) emit more short-wavelength radiation. Since the upper atmosphere is not homogeneous and contains significant magnetic structure, the solar ultraviolet (UV), EUV and X-ray flux varies markedly over the cycle.

The photo montage to the left illustrates this variation for soft X-ray, as observed by the Japanese satellite Yohkoh from after August 30, 1991, at the peak of cycle 22, to September 6, 2001, at the peak of cycle 23. Similar cycle-related variations are observed in the flux of solar UV or EUV radiation, as observed, for example, by the SOHO or TRACE satellites.

Even though it only accounts for a minuscule fraction of total solar radiation, the impact of solar UV, EUV and X-ray radiation on the Earth's upper atmosphere is profound. Solar UV flux is a major driver of stratospheric chemistry, and increases in ionizing radiation significantly affect ionosphere-influenced temperature and electrical conductivity.

Solar radio flux

edit

Emission from the Sun at centimetric (radio) wavelength is due primarily to coronal plasma trapped in the magnetic fields overlying active regions.[81] The F10.7 index is a measure of the solar radio flux per unit frequency at a wavelength of 10.7 cm, near the peak of the observed solar radio emission. F10.7 is often expressed in SFU or solar flux units (1 SFU = 10−22 W m−2 Hz−1). It represents a measure of diffuse, nonradiative coronal plasma heating. It is an excellent indicator of overall solar activity levels and correlates well with solar UV emissions.

Sunspot activity has a major effect on long distance radio communications, particularly on the shortwave bands although medium wave and low VHF frequencies are also affected. High levels of sunspot activity lead to improved signal propagation on higher frequency bands, although they also increase the levels of solar noise and ionospheric disturbances. These effects are caused by impact of the increased level of solar radiation on the ionosphere.

10.7 cm solar flux could interfere with point-to-point terrestrial communications.[82]

Clouds

edit

Speculations about the effects of cosmic-ray changes over the cycle potentially include:

  • Changes in ionization affect the aerosol abundance that serves as the condensation nucleus for cloud formation.[83] During solar minima more cosmic rays reach Earth, potentially creating ultra-small aerosol particles as precursors to cloud condensation nuclei.[84] Clouds formed from greater amounts of condensation nuclei are brighter, longer lived and likely to produce less precipitation.
  • A change in cosmic rays could affect certain types of clouds.[85]
  • It was proposed that, particularly at high latitudes, cosmic ray variation may impact terrestrial low altitude cloud cover (unlike a lack of correlation with high altitude clouds), partially influenced by the solar-driven interplanetary magnetic field (as well as passage through the galactic arms over longer timeframes),[86][87][88][89] but this hypothesis was not confirmed.[90]

Later papers showed that production of clouds via cosmic rays could not be explained by nucleation particles. Accelerator results failed to produce sufficient, and sufficiently large, particles to result in cloud formation;[91][92] this includes observations after a major solar storm.[93] Observations after Chernobyl do not show any induced clouds.[94]

Terrestrial

edit

Organisms

edit

The impact of the solar cycle on living organisms has been investigated (see chronobiology). Some researchers claim to have found connections with human health.[95]

The amount of ultraviolet UVB light at 300 nm reaching the Earth's surface varies by a few percent over the solar cycle due to variations in the protective ozone layer. In the stratosphere, ozone is continuously regenerated by the splitting of O2 molecules by ultraviolet light. During a solar minimum, the decrease in ultraviolet light received from the Sun leads to a decrease in the concentration of ozone, allowing increased UVB to reach the Earth's surface.[96][97]

Radio communication

edit
Main article: Skywave

Skywave modes of radio communication operate by bending (refracting) radio waves (electromagnetic radiation) through the Ionosphere. During the "peaks" of the solar cycle, the ionosphere becomes increasingly ionized by solar photons and cosmic rays. This affects the propagation of the radio wave in complex ways that can either facilitate or hinder communications. Forecasting of skywave modes is of considerable interest to commercial marine and aircraft communications, amateur radio operators and shortwave broadcasters. These users occupy frequencies within the High Frequency or 'HF' radio spectrum that are most affected by these solar and ionospheric variances. Changes in solar output affect the maximum usable frequency, a limit on the highest frequency usable for communications.

Climate

edit

Both long-term and short-term variations in solar activity are proposed to potentially affect global climate, but it has proven challenging to show any link between solar variation and climate.[2]

Early research attempted to correlate weather with limited success,[98] followed by attempts to correlate solar activity with global temperature. The cycle also impacts regional climate. Measurements from the SORCE's Spectral Irradiance Monitor show that solar UV variability produces, for example, colder winters in the U.S. and northern Europe and warmer winters in Canada and southern Europe during solar minima.[99]

Three proposed mechanisms mediate solar variations' climate impacts:

  • Total solar irradiance ("Radiative forcing").
  • Ultraviolet irradiance. The UV component varies by more than the total, so if UV were for some (as yet unknown) reason having a disproportionate effect, this might affect climate.
  • Solar wind-mediated galactic cosmic ray changes, which may affect cloud cover.

The solar cycle variation of 0.1% has small but detectable effects on the Earth's climate.[100][101][102] Camp and Tung suggest that solar irradiance correlates with a variation of 0.18 K ±0.08 K (0.32 °F ±0.14 °F) in measured average global temperature between solar maximum and minimum.[103]

Other effects include one study which found a relationship with wheat prices,[104] and another one that found a weak correlation with the flow of water in the Paraná River.[105] Eleven-year cycles have been found in tree-ring thicknesses[14] and layers at the bottom of a lake[15] hundreds of millions of years ago.

The current scientific consensus on climate change is that solar variations only play a marginal role in driving global climate change,[2] since the measured magnitude of recent solar variation is much smaller than the forcing due to greenhouse gases.[3] Also, average solar activity in the 2010s was no higher than in the 1950s (see above), whereas average global temperatures had risen markedly over that period. Otherwise, the level of understanding of solar impacts on weather is low.[106]

Solar variations also affect the orbital decay of objects in low Earth orbit (LEO) by altering the density of the upper thermosphere.[107]

Solar dynamo

edit
Main article: Solar dynamo

The 11-year solar cycle is thought to be one-half of a 22-year Babcock–Leighton solar dynamo cycle, which corresponds to an oscillatory exchange of energy between toroidal and poloidal solar magnetic fields which is mediated by solar plasma flows which also provides energy to the dynamo system at every step. At solar-cycle maximum, the external poloidal dipolar magnetic field is near its dynamo-cycle minimum strength, but an internal toroidal quadrupolar field, generated through differential rotation within the tachocline, is near its maximum strength. At this point in the dynamo cycle, buoyant upwelling within the Convection zone forces emergence of the toroidal magnetic field through the photosphere, giving rise to pairs of sunspots, roughly aligned east–west with opposite magnetic polarities. The magnetic polarity of sunspot pairs alternates every solar cycle, a phenomenon described by Hale's law.[108][109]

During the solar cycle's declining phase, energy shifts from the internal toroidal magnetic field to the external poloidal field, and sunspots diminish in number. At solar minimum, the toroidal field is, correspondingly, at minimum strength, sunspots are relatively rare and the poloidal field is at maximum strength. During the next cycle, differential rotation converts magnetic energy back from the poloidal to the toroidal field, with a polarity that is opposite to the previous cycle. The process carries on continuously, and in an idealized, simplified scenario, each 11-year sunspot cycle corresponds to a change in the polarity of the Sun's large-scale magnetic field.[110][111]

Solar dynamo models indicate that plasma flux transport processes in the solar interior such as differential rotation, meridional circulation and turbulent pumping play an important role in the recycling of the toroidal and poloidal components of the solar magnetic field.[112] The relative strengths of these flux transport processes also determine the "memory" of the solar cycle that plays an important role in physics-based predictions of the solar cycle. In particular, stochastically forced non-linear solar dynamo simulations establish that the solar cycle memory is short, lasting over one cycle, thus implying accurate predictions are possible only for the next solar cycle and not beyond.[113][114] This postulate of a short one cycle memory in the solar dynamo mechanism was later observationally verified.[115]

Although the tachocline has long been thought to be the key to generating the Sun's large-scale magnetic field, recent research has questioned this assumption. Radio observations of brown dwarfs have indicated that they also maintain large-scale magnetic fields and may display cycles of magnetic activity. The Sun has a radiative core surrounded by a convective envelope, and at the boundary of these two is the tachocline. However, brown dwarfs lack radiative cores and tachoclines. Their structure consists of a solar-like convective envelope that exists from core to surface. Since they lack a tachocline yet still display solar-like magnetic activity, it has been suggested that solar magnetic activity is only generated in the convective envelope.[116]

Speculated influence of the planets

edit

A 2012 paper proposed that the torque exerted by the planets on a non-spherical tachocline layer deep in the Sun may synchronize the solar dynamo.[117] Their results were shown to be an artifact of the incorrectly applied smoothing method leading to aliasing.[118] Additional models incorporating the influence of planetary forces on the Sun have since been proposed.[119] However, the solar variability is known to be essentially stochastic and unpredictable beyond one solar cycle, which contradicts the idea of the deterministic planetary influence on solar dynamo.[120] Modern dynamo models are able to reproduce the solar cycle without any planetary influence.[23]

In 1974 the book The Jupiter Effect suggested that the alignment of the planets would alter the Sun's solar wind and, in turn, Earth's weather, culminating in multiple catastrophes on March 10, 1982. None of the catastrophes occurred. In 2023, a paper by Cionco et al. demonstrated the improbability that the suspected tidal effect on the Sun driven by Venus and Jupiter were significant on whole solar tidal generating potential.[121]

See also

edit

References

edit
  1. ^ "NASA/Marshall Solar Physics". nasa.gov. Retrieved 2015-11-17.   This article incorporates text from this source, which is in the public domain.[dead link]
  2. ^ a b c Joanna D. Haigh "The Sun and the Earth's Climate", Living Reviews in Solar Physics (access date 31 January 2012)
  3. ^ a b Houghton, J.T.; Ding, Y.; Griggs, D.J.; Noguer, M., eds. (2001). "6.11 Total Solar Irradiance—Figure 6.6: Global, annual mean radiative forcings (1750 to present)". Climate Change 2001: Working Group I: The Scientific Basis. Intergovernmental Panel on Climate Change. Retrieved 2007-04-15.; see also the IPCC Fourth Assessment Report, in which the magnitude of variation in solar irradiance was revised downward, although the evidence of connections between solar variation and certain aspects of climate increased over the same time period: Assessment Report-4, Working group 1, chapter 2 Archived 2013-12-07 at the Wayback Machine
  4. ^ Karoff, Christoffer; Jørgensen, Carsten Sønderskov; Senthamizh Pavai, V.; Arlt, Rainer (12 June 2019). "Christian Horrebow's Sunspot Observations – II. Construction of a Record of Sunspot Positions". Solar Physics. 294 (6): 77. arXiv:1906.10895. Bibcode:2019SoPh..294...78K. doi:10.1007/s11207-019-1466-y. S2CID 189841594.
  5. ^ a b Schwabe (1843). "Sonnenbeobachtungen im Jahre 1843" [Observations of the sun in the year 1843]. Astronomische Nachrichten (in German). 21: 233–236. From page 235: "Vergleicht man nun die Zahl der Gruppen und der flecken-freien Tage mit einander, so findet man, dass die Sonnenflecken eine Periode von ungefähr 10 Jahren hatten" ('If one compares the number of groups [of sunspots] and the sunspot-free days with one another, then one finds that the sunspots had a period of about 10 years')
  6. ^ Wolf, R. (1852). "Neue untersuchungen über die periode der sonnenflecken und ihre bedeutung" [New investigations regarding the period of sunspots and its significance]. Mittheilungen der Naturforschenden Gesellschaft in Bern (in German). 255: 249–270.
  7. ^ Eddy, John A. (June 1976). "The Maunder Minimum". Science. 192 (4245): 1189–1202. Bibcode:1976Sci...192.1189E. doi:10.1126/science.192.4245.1189. JSTOR 1742583. PMID 17771739. S2CID 33896851.
  8. ^ a b c d e David H. Hathaway, "The Solar Cycle", Living Reviews in Solar Physics, March 2010, Max Planck Institute for Solar System Research, Katlenburg-Lindau, Germany. ISSN 1614-4961 (accessed 19 July 2015)
  9. ^ "Sunspot Number graphics". Solar Influences Data Analysis Center. Royal Observatory of Belgium.
  10. ^ Wu, C.J.; Krivova, N.; Solanki, S.K.; Usoskin, I.G. (2018). "Solar total and spectral irradiance reconstruction over the last 9000 years". Astronomy & Astrophysics. 620: A120. arXiv:1811.03464. Bibcode:2018A&A...620A.120W. doi:10.1051/0004-6361/201832956.
  11. ^ a b Usoskin, Ilya G.; Solanki, Sami K.; Kovaltsov, Gennady A. (2007). "Grand minima and maxima of solar activity: New observational constraints" (PDF). Astron. Astrophys. 471 (1): 301–309. arXiv:0706.0385. Bibcode:2007A&A...471..301U. doi:10.1051/0004-6361:20077704. S2CID 7742132.
  12. ^ a b Solanki, Sami K.; Usoskin, Ilya G.; Kromer, Bernd; Schüssler, Manfred; Beer, Jürg (2004). "Unusual activity of the Sun during recent decades compared to the previous 11,000 years" (PDF). Nature. 431 (7012): 1084–1087. Bibcode:2004Natur.431.1084S. doi:10.1038/nature02995. PMID 15510145. S2CID 4373732. Retrieved 2007-04-17., "11,000 Year Sunspot Number Reconstruction". Global Change Master Directory. Archived from the original on 2015-11-02. Retrieved 2005-03-11.
  13. ^ Usoskin, Ilya G.; Solanki, Sami K.; Schüssler, Manfred; Mursula, Kalevi; Alanko, Katja (2003). "A Millennium Scale Sunspot Number Reconstruction: Evidence For an Unusually Active Sun Since the 1940s". Physical Review Letters. 91 (21): 211101. arXiv:astro-ph/0310823. Bibcode:2003PhRvL..91u1101U. doi:10.1103/PhysRevLett.91.211101. PMID 14683287. S2CID 20754479.
  14. ^ a b Luthardt, Ludwig; Rößler, Ronny (February 2017). "Fossil forest reveals sunspot activity in the early Permian". Geology. 45 (2): 279. Bibcode:2017Geo....45..279L. doi:10.1130/G38669.1. S2CID 132999292.
  15. ^ a b Li, Pengbo; et al. (September 2018). "Sunspot cycles recorded in siliciclastic biolaminites at the dawn of the Neoproterozoic Sturtian glaciation in South China". Precambrian Research. 315: 75–91. Bibcode:2018PreR..315...75L. doi:10.1016/j.precamres.2018.07.018. S2CID 135344975.
  16. ^ Michael Marshall (18 August 2018). "Rock layers show our sun has been in same cycle for 700 million years". New Scientist.
  17. ^ Celia Martin-Puertas; Katja Matthes; Achim Brauer; Raimund Muscheler; Felicitas Hansen; Christof Petrick; Ala Aldahan; Göran Possnert; Bas van Geel (2 April 2012). "Regional atmospheric circulation shifts induced by a grand solar minimum". Nature Geoscience. 5 (6): 397–401. Bibcode:2012NatGe...5..397M. doi:10.1038/ngeo1460.
  18. ^ Usoskin, I. G.; Mursula, K.; Arlt, R.; Kovaltsov, G. A. (2009). "A solar cycle lost in 1793–1800: Early sunspot observations resolve the old mystery". The Astrophysical Journal. 700 (2): L154. arXiv:0907.0063. Bibcode:2009ApJ...700L.154U. doi:10.1088/0004-637X/700/2/L154. S2CID 14882350.
  19. ^ "Centuries-old sketches solve sunspot mystery". New Scientist. 1 August 2009. p. 10.
  20. ^ Brauer, Achim; Possnert, Göran; Aldahan, Ala; Błaszkiewicz, Mirosław; Słowinski, Michał; Ott, Florian; Dräger, Nadine; Mekhaldi, Florian; Adolphi, Florian (31 May 2018). "Synchronizing 10Be in two varved lake sediment records to IntCal13 14C during three grand solar minima". Climate of the Past. 14 (5): 687–696. Bibcode:2018CliPa..14..687C. doi:10.5194/cp-14-687-2018. hdl:21.11116/0000-0003-2C5D-5. ISSN 1814-9324.
  21. ^ a b National Weather Service. "Hello Solar Cycle 25". Retrieved 2020-09-15.
  22. ^ for example: "ADS search for "solar sunspot cycle 25 prediction"". Retrieved 2020-03-17.
  23. ^ a b Bhowmik, Prantika; Nandy, Dibyendu (6 December 2018). "Prediction of the strength and timing of sunspot cycle 25 reveal decadal-scale space environmental conditions". Nature Communications. 9 (1): 5209. arXiv:1909.04537. Bibcode:2018NatCo...9.5209B. doi:10.1038/s41467-018-07690-0. ISSN 2041-1723. PMC 6283837. PMID 30523260.
  24. ^ "Solar Cycle 25 Preliminary Forecast". NOAA / NWS Space Weather Prediction Center.
  25. ^ Bernhard Fleck (14 January 2008). "SOHO: the new solar cycle starts with a 'bang'". European Space Agency (Press release). Retrieved 2017-05-11.
  26. ^ Tony Phillips (10 January 2008). "Solar Cycle 24 begins". NASA. Archived from the original on 2021-02-28. Retrieved 2010-05-29.
  27. ^ Tony Phillips (4 June 2010). "As the Sun Awakens, NASA Keeps a Wary Eye on Space Weather". NASA. Archived from the original on 2021-03-20. Retrieved 2013-05-18.
  28. ^ "Solar Cycle Progression". NOAA / NWS Space Weather Prediction Center. Retrieved 2015-07-06.
  29. ^ "Sunspot Number | SILSO". www.sidc.be.
  30. ^ "Spotless Days".
  31. ^ "What's wrong with the Sun? (Nothing) more information: Spotless Days". Archived from the original on 2008-07-14.
  32. ^ "Solaemon's Spotless Days Page". Archived from the original on 2017-07-22. Retrieved 2015-08-15.
  33. ^ "NASA – Sun-Earth Day – Technology Through Time – Greece". sunearthday.nasa.gov.
  34. ^ Willson, Richard C.; H.S. Hudson (1991). "The Sun's luminosity over a complete solar cycle". Nature. 351 (6321): 42–4. Bibcode:1991Natur.351...42W. doi:10.1038/351042a0. S2CID 4273483.
  35. ^ Willson RC, Gulkis S, Janssen M, Hudson HS, Chapman GA (February 1981). "Observations of Solar Irradiance Variability". Science. 211 (4483): 700–2. Bibcode:1981Sci...211..700W. doi:10.1126/science.211.4483.700. PMID 17776650.
  36. ^ Chatzistergos, Theodosios; Krivova, Natalie A.; Ermolli, Ilaria (17 November 2022). "Full-disc Ca ii K observations—A window to past solar magnetism". Frontiers in Astronomy and Space Sciences. 9: 1038949. arXiv:2210.13285. Bibcode:2022FrASS...938949C. doi:10.3389/fspas.2022.1038949. ISSN 2296-987X.
  37. ^ Chatzistergos T, Ermolli I, Krivova NA, Solanki SK, Banerjee D, Barata T, Belik M, et al. (July 2020). "Analysis of full-disc Ca II K spectroheliograms – III. Plage area composite series covering 1892–2019". Astronomy and Astrophysics. 639: A88. arXiv:2005.01435. Bibcode:2020A&A...639A..88C. doi:10.1051/0004-6361/202037746. S2CID 218487277.
  38. ^ Chatzistergos, Theodosios; Ermolli, Ilaria; Krivova, Natalie A.; Barata, Teresa; Carvalho, Sara; Malherbe, Jean-Marie (November 2022). "Scrutinising the relationship between plage areas and sunspot areas and numbers". Astronomy & Astrophysics. 667: A167. arXiv:2209.07077. Bibcode:2022A&A...667A.167C. doi:10.1051/0004-6361/202244913. ISSN 0004-6361. S2CID 252280541.
  39. ^ Chatzistergos, Theodosios; Ermolli, Ilaria; Solanki, Sami K.; Krivova, Natalie A.; Giorgi, Fabrizio; Yeo, Kok Leng (June 2019). "Recovering the unsigned photospheric magnetic field from Ca II K observations". Astronomy & Astrophysics. 626: A114. arXiv:1905.03453. Bibcode:2019A&A...626A.114C. doi:10.1051/0004-6361/201935131. ISSN 0004-6361. S2CID 148571864.
  40. ^ Babcock, Horace W.; Babcock, Harold D. (March 1955). "The Sun's Magnetic Field, 1952–1954". The Astrophysical Journal. 121: 349. Bibcode:1955ApJ...121..349B. doi:10.1086/145994. ISSN 0004-637X.
  41. ^ Owens, Mathew J.; Lockwood, Mike; Barnard, Luke A.; Scott, Chris J.; Haines, Carl; Macneil, Allan (20 May 2021). "Extreme Space-Weather Events and the Solar Cycle". Solar Physics. 296 (5): 82. Bibcode:2021SoPh..296...82O. doi:10.1007/s11207-021-01831-3. ISSN 1573-093X. S2CID 236402345.
  42. ^ Owens, Mathew J.; Barnard, Luke A.; Pope, Benjamin J. S.; Lockwood, Mike; Usoskin, Ilya; Asvestari, Eleanna (19 August 2022). "Solar Energetic-Particle Ground-Level Enhancements and the Solar Cycle". Solar Physics. 297 (8): 105. arXiv:2207.12787. Bibcode:2022SoPh..297..105O. doi:10.1007/s11207-022-02037-x. ISSN 1573-093X. S2CID 251066764.
  43. ^ "The Most Powerful Solar Flares Ever Recorded". Spaceweather.com.
  44. ^ "Extreme Space Weather Events". National Geophysical Data Center. Retrieved 2015-11-17.
  45. ^ Du, Zhan-Le; Wang, Hua-Ning; He, Xiang-Tao (2006). "The Relation between the Amplitude and the Period of Solar Cycles". Chinese Journal of Astronomy and Astrophysics. 6 (4): 489–494. Bibcode:2006ChJAA...6..489D. doi:10.1088/1009-9271/6/4/12. S2CID 73563204.
  46. ^ Waldmeier M., 1939, Astron. Mitt. Zurich, 14, 439
  47. ^ Sonett, C. P.; Finney, S. A.; Berger, A. (24 April 1990). "The Spectrum of Radiocarbon". Philosophical Transactions of the Royal Society A. 330 (1615): 413–26. Bibcode:1990RSPTA.330..413S. doi:10.1098/rsta.1990.0022. S2CID 123641430.
  48. ^ a b Braun, H; Christl, M; Rahmstorf, S; Ganopolski, A; Mangini, A; Kubatzki, C; Roth, K; Kromer, B (10 November 2005). "Possible solar origin of the 1,470-year glacial climate cycle demonstrated in a coupled model" (PDF). Nature. 438 (7065): 208–11. Bibcode:2005Natur.438..208B. doi:10.1038/nature04121. PMID 16281042. S2CID 4346459.
  49. ^ Hathaway, David H.; Wilson, Robert M. (2004). "What the Sunspot Record Tells Us About Space Climate" (PDF). Solar Physics. 224 (1–2): 5–19. Bibcode:2004SoPh..224....5H. doi:10.1007/s11207-005-3996-8. S2CID 55971262. Archived from the original (PDF) on 2006-01-04. Retrieved 2007-04-19.
  50. ^ Usoskin I.G. (2017). "A History of Solar Activity over Millennia". Living Reviews in Solar Physics. 14 (3): 3. arXiv:0810.3972. Bibcode:2017LRSP...14....3U. doi:10.1007/s41116-017-0006-9. S2CID 195340740. PDF Copy
  51. ^ Lockwood M. (2013). "Reconstruction and Prediction of Variations in the Open Solar Magnetic Flux and Interplanetary Conditions". Living Reviews in Solar Physics. 10 (4): 4. Bibcode:2013LRSP...10....4L. doi:10.12942/lrsp-2013-4. PDF Copy
  52. ^ Owens M.J. & Forsyth R.J. (2013). "The Heliospheric Magnetic Field". Living Reviews in Solar Physics. 10 (5): 5. arXiv:1002.2934. Bibcode:2013LRSP...10....5O. doi:10.12942/lrsp-2013-5. S2CID 122870891.
  53. ^ "The Sun and Climate" (PDF). U.S. Geological Survey. Fact Sheet 0095-00. Retrieved 2015-11-17.
  54. ^ Vasiliev, S. S.; Dergachev, V. A. (2002). "The ~ 2400-year cycle in atmospheric radiocarbon concentration: bispectrum of 14C data over the last 8000 years". Annales Geophysicae. 20 (1): 115–20. Bibcode:2002AnGeo..20..115V. doi:10.5194/angeo-20-115-2002.
  55. ^ Usoskin IG, Gallet Y, Lopes F, Kovaltsov GA, Hulot G (2016). "Solar activity during the Holocene: the Hallstatt cycle and its consequence for grand minima and maxima". Astron. Astrophys. 587. A150. arXiv:1602.02483. Bibcode:2016A&A...587A.150U. doi:10.1051/0004-6361/201527295. S2CID 55007495.
  56. ^ Scafetta, Nicola; Milani, Franco; Bianchini, Antonio; Ortolani, Sergio (2016). "On the astronomical origin of the Hallstatt oscillation found in radiocarbon and climate records throughout the Holocene". Earth-Science Reviews. 162: 24–43. arXiv:1610.03096. Bibcode:2016ESRv..162...24S. doi:10.1016/j.earscirev.2016.09.004. S2CID 119155024.
  57. ^ Damon, Paul E.; Jirikowic, John L. (31 March 2006). "The Sun as a low-frequency harmonic oscillator". Radiocarbon. 34 (2): 199–205. doi:10.2458/azu_js_rc.34.1450. ISSN 0033-8222.
  58. ^ Damon, Paul E., and Sonett, Charles P., "Solar and terrestrial components of the atmospheric C-14 variation spectrum," In The Sun in Time, Vol. 1, pp. 360–388, University of Arizona Press, Tucson AZ (1991). Abstract (accessed 16 July 2015)
  59. ^ see table in "Solar Variability: climatic change resulting from changes in the amount of solar energy reaching the upper atmosphere". Introduction to Quaternary Ecology. Archived from the original on 2005-03-20. Retrieved 2015-07-16.
  60. ^ Past Interglacials Working Group of PAGES (2016). "Interglacials of the last 800,000 years". Reviews of Geophysics. 54 (1): 162–219. Bibcode:2016RvGeo..54..162P. doi:10.1002/2015RG000482. hdl:10261/168880. ISSN 8755-1209.
  61. ^ Viaggi, P. (2021). "Quantitative impact of astronomical and sun-related cycles on the Pleistocene climate system from Antarctica records". Quaternary Science Advances. 4: 100037. Bibcode:2021QSAdv...400037V. doi:10.1016/j.qsa.2021.100037. ISSN 2666-0334.
  62. ^ Wolfgang Gleißberg (1953). Die Häufigkeit der Sonnenflecken (in German). Berlin: Ahademie Verlag.
  63. ^ Potgeiter, M. (2013). "Solar Modulation of Cosmic Rays". Living Reviews in Solar Physics. 10 (1): 3. arXiv:1306.4421. Bibcode:2013LRSP...10....3P. doi:10.12942/lrsp-2013-3. S2CID 56546254.
  64. ^ Solanki, Sami K.; Usoskin, Ilya G.; Kromer, Bernd; Schüssler, Manfred; Beer, Jürg (2004). "Unusual activity of the Sun during recent decades compared to the previous 11,000 years" (PDF). Nature. 431 (7012): 1084–7. Bibcode:2004Natur.431.1084S. doi:10.1038/nature02995. PMID 15510145. S2CID 4373732.
  65. ^ Kopp G (1 July 2016). "Magnitudes and timescales of total solar irradiance variability". Journal of Space Weather and Space Climate. 6: A30. arXiv:1606.05258. Bibcode:2016JSWSC...6A..30K. doi:10.1051/swsc/2016025.
  66. ^ Richard C. Willson (16 May 2014). "ACRIM3 and the Total Solar Irradiance database". Astrophysics and Space Science. 352 (2): 341–352. Bibcode:2014Ap&SS.352..341W. doi:10.1007/s10509-014-1961-4.
  67. ^ Krivova NA, Solanki SK, Wenzler T (1 October 2009). "ACRIM-gap and total solar irradiance revisited: Is there a secular trend between 1986 and 1996?". Geophysical Research Letters. 36 (20): L20101. arXiv:0911.3817. Bibcode:2009GeoRL..3620101K. doi:10.1029/2009GL040707.
  68. ^ Amdur, T.; Huybers, P. (16 August 2023). "A Bayesian Model for Inferring Total Solar Irradiance From Proxies and Direct Observations: Application to the ACRIM Gap". Journal of Geophysical Research: Atmospheres. 128 (15). Bibcode:2023JGRD..12838941A. doi:10.1029/2023JD038941. ISSN 2169-897X. S2CID 260264050.
  69. ^ Willson, R.C.; et al. (1981). "Observations of Solar Irradiance Variability". Science. 211 (4483): 700–2. Bibcode:1981Sci...211..700W. doi:10.1126/science.211.4483.700. PMID 17776650.
  70. ^ K.L. Yeo; et al. (23 September 2014). "Reconstruction of total and spectral solar irradiance from 1974 to 2013 based on KPVT, SoHO/MDI and SDO/HMI observations". Astronomy & Astrophysics. 570: A85. arXiv:1408.1229. Bibcode:2014A&A...570A..85Y. doi:10.1051/0004-6361/201423628. S2CID 56424234.
  71. ^ Haigh, J. D; Winning, A. R; Toumi, R; Harder, J. W (6 October 2010). "An influence of solar spectral variations on radiative forcing of climate" (PDF). Nature. 467 (7316): 696–9. Bibcode:2010Natur.467..696H. doi:10.1038/nature09426. hdl:10044/1/18858. PMID 20930841. S2CID 4320984.
  72. ^ Willson RC; Hudson HS (1991). "The Sun's luminosity over a complete solar cycle". Nature. 351 (6321): 42–4. Bibcode:1991Natur.351...42W. doi:10.1038/351042a0. S2CID 4273483.
  73. ^ Willson, Richard C. (2014). "ACRIM3 and the Total Solar Irradiance database". Astrophysics and Space Science. 352 (2): 341–352. Bibcode:2014Ap&SS.352..341W. doi:10.1007/s10509-014-1961-4.
  74. ^ Willson R.C.; Gulkis S.; Janssen M.; Hudson H.S.; Chapman G.A. (1981). "Observations of solar irradiance variability". Science. 211 (4483): 700–2. Bibcode:1981Sci...211..700W. doi:10.1126/science.211.4483.700. PMID 17776650.
  75. ^ "Total Solar Irradiance Graph from ACRIM page". ACRIM project web page. Archived from the original on 2015-10-17. Retrieved 2015-11-17.
  76. ^ Willson R.C.; Mordvinov A.V. (2003). "Secular total solar irradiance trend during solar cycles 21–23". Geophys. Res. Lett. 30 (5): 1199. Bibcode:2003GeoRL..30.1199W. doi:10.1029/2002GL016038. S2CID 55755495.
  77. ^ Scafetta N.; Willson R.C. (2009). "ACRIM-gap and TSI trend issue resolved using a surface magnetic flux TSI proxy model". Geophys. Res. Lett. 36 (5): L05701. Bibcode:2009GeoRL..36.5701S. doi:10.1029/2008GL036307. S2CID 7160875.
  78. ^ Chatzistergos T, Krivova NA, Ermolli I, Kok Leng Y, Mandal S, Solanki SK, Kopp G, Malherbe JM (1 December 2021). "Reconstructing solar irradiance from historical Ca II K observations. I. Method and its validation". Astronomy and Astrophysics. 656: A104. arXiv:2109.05844. Bibcode:2021A&A...656A.104C. doi:10.1051/0004-6361/202141516.
  79. ^ Solanki SK, Schuessler M, Fligge M (1 February 2002). "Secular variation of the Sun's magnetic flux". Astronomy and Astrophysics. 383 (2): 706–712. Bibcode:2002A&A...383..706S. doi:10.1051/0004-6361:20011790.
  80. ^ Haigh, J D (17 May 1996). "The Impact of Solar Variability on Climate". Science. 272 (5264): 981–984. Bibcode:1996Sci...272..981H. doi:10.1126/science.272.5264.981. PMID 8662582. S2CID 140647147.
  81. ^ Tapping K.F. (1987). "Recent solar radio astronomy at centimeter wavelength: the temporal variability of the 10.7-cm flux". J. Geophys. Res. 92 (D1): 829–838. Bibcode:1987JGR....92..829T. doi:10.1029/JD092iD01p00829.
  82. ^ "The Effect of 10.7 cm Solar Radiation on 2.4 GHz Digital Spread Spectrum Communications". NARTE News. 17 (3). July–October 1999.
  83. ^ Tinsley, Brian A.; Yu, Fangqun (2004). "Atmospheric Ionization and Clouds as Links Between Solar Activity and Climate" (PDF). In Pap, Judit M.; Fox, Peter (eds.). Solar Variability and its Effects on Climate. Geophysical monograph series. Vol. 141. American Geophysical Union. pp. 321–339. Bibcode:2004GMS...141..321T. CiteSeerX 10.1.1.175.5237. doi:10.1029/141GM22. ISBN 978-0-87590-406-1. Archived from the original (PDF) on 2007-06-04. Retrieved 2015-08-10."Department of Physics – the University of Texas at Dallas". Archived from the original on 2015-08-15. Retrieved 2015-08-10.
  84. ^ "CERN's CLOUD experiment provides unprecedented insight into cloud formation" (Press release). CERN. 25 August 2011. Retrieved 2016-11-12.
  85. ^ Kumar, Vinay; Dhaka, Surendra K.; Hitchman, Matthew H.; Yoden, Shigeo (6 March 2023). "The influence of solar-modulated regional circulations and galactic cosmic rays on global cloud distribution". Scientific Reports. 13 (1): 3707. Bibcode:2023NatSR..13.3707K. doi:10.1038/s41598-023-30447-9. ISSN 2045-2322. PMC 9988889. PMID 36878955.
  86. ^ Shaviv, Nir J (2005). "On climate response to changes in the cosmic ray flux and radiative budget" (PDF). Journal of Geophysical Research. 110 (A08105): A08105. arXiv:physics/0409123. Bibcode:2005JGRA..110.8105S. doi:10.1029/2004JA010866. S2CID 16364672. Retrieved 2011-06-17.
  87. ^ Svensmark, Henrik (2007). "Cosmoclimatology: a new theory emerges". Astronomy & Geophysics. 48 (1): 1.18–1.24. Bibcode:2007A&G....48a..18S. doi:10.1111/j.1468-4004.2007.48118.x.
  88. ^ Svensmark, Henrik (1998). "Influence of Cosmic Rays on Earth's Climate" (PDF). Physical Review Letters. 81 (22): 5027–5030. Bibcode:1998PhRvL..81.5027S. CiteSeerX 10.1.1.522.585. doi:10.1103/PhysRevLett.81.5027. Retrieved 2011-06-17.
  89. ^ Shaviv, Nir J & Veizer, Ján (2003). "Celestial driver of Phanerozoic climate?". Geological Society of America. 13 (7): 4. Bibcode:2003GSAT...13g...4S. doi:10.1130/1052-5173(2003)013<0004:CDOPC>2.0.CO;2.
  90. ^ Sun, B.; Bradley, R. (2002). "Solar influences on cosmic rays and cloud formation: A reassessment". Journal of Geophysical Research. 107 (D14): 4211. Bibcode:2002JGRD..107.4211S. doi:10.1029/2001jd000560.
  91. ^ Pierce, J.; Adams, P. (2009). "Can cosmic rays affect cloud condensation nuclei by altering new particle formation rates?". Geophysical Research Letters. 36 (9): 36. Bibcode:2009GeoRL..36.9820P. doi:10.1029/2009gl037946. S2CID 15704833.
  92. ^ Snow-Kropla, E.; et al. (April 2011). "Cosmic rays, aerosol formation and cloud-condensation nuclei: sensitivities to model uncertainties". Atmospheric Chemistry and Physics. 11 (8): 4001. Bibcode:2011ACP....11.4001S. doi:10.5194/acp-11-4001-2011.
  93. ^ Erlykin, A.; et al. (August 2013). "A review of the relevance of the 'CLOUD' results and other recent observations to the possible effect of cosmic rays on the terrestrial climate". Meteorology and Atmospheric Physics. 121 (3): 137. arXiv:1308.5067. Bibcode:2013MAP...121..137E. doi:10.1007/s00703-013-0260-x. S2CID 118515392.
  94. ^ Sloan, T.; Wolfendale, A. (June 2007). "Cosmic Rays and Global Warming". 30TH INTERNATIONAL COSMIC RAY CONFERENCE, Merida, Mexico.
  95. ^ Halberg, F; Cornélissen, G; Otsuka, K; Watanabe, Y; Katinas, GS; Burioka, N; Delyukov, A; Gorgo, Y; Zhao, Z (2000). "Cross-spectrally coherent ~10.5- and 21-year biological and physical cycles, magnetic storms and myocardial infarctions". Neuroendocrinology Letters. 21 (3): 233–258. PMID 11455355. Archived from the original on 2008-07-29.
  96. ^ National Research Council (1994). "Solar Variations, Ozone, and the Middle Atmosphere". Solar Influences on Global Change. Washington DC: National Academies Press. pp. 66–68. doi:10.17226/4778. hdl:2060/19950005971. ISBN 978-0-309-05148-4.
  97. ^ Echer, E; Kirchhoff, VWJH; Sahai, Y; Paes Leme, N (2001). "A study of the solar cycle signal on total ozone over low-latitude Brazilian observation stations". Advances in Space Research. 27 (12): 1983–1986. Bibcode:2001AdSpR..27.1983E. doi:10.1016/S0273-1177(01)00270-8.
  98. ^ Weart, Spencer (2003). "Changing Sun, Changing Climate?". The Discovery of Global Warming. Harvard University Press. ISBN 978-0-674-01157-1. Archived from the original on 2011-08-04. Retrieved 2008-04-17.
  99. ^ Ineson S.; Scaife A.A.; Knight J.R.; Manners J.C.; Dunstone N.J.; Gray L.J.; Haigh J.D. (9 October 2011). "Solar forcing of winter climate variability in the Northern Hemisphere" (PDF). Nature Geoscience. 4 (11): 753–7. Bibcode:2011NatGe...4..753I. doi:10.1038/ngeo1282. hdl:10044/1/18859.
  100. ^ Labitzke K.; Matthes K. (2003). "Eleven-year solar cycle variations in the atmosphere: observations, mechanisms and models". The Holocene. 13 (3): 311–7. Bibcode:2003Holoc..13..311L. doi:10.1191/0959683603hl623rp. S2CID 129100529.
  101. ^ Pablo J.D. Mauas & Andrea P. Buccino. "Long-term solar activity influences on South American rivers" page 5. Journal of Atmospheric and Solar-Ter restrial Physics on Space Climate, March 2010. Accessed: 20 September 2014.
  102. ^ Zanchettin, D.; Rubino, A.; Traverso, P.; Tomasino, M. (2008). "[Impact of variations in solar activity on hydrological decadal patterns in northern Italy]". Journal of Geophysical Research. 113 (D12): D12102. Bibcode:2008JGRD..11312102Z. doi:10.1029/2007JD009157. S2CID 54975234.
  103. ^ C. D. Camp & K. K. Tung (2007). "Surface warming by the solar cycle as revealed by the composite mean difference projection". Geophysical Research Letters. 34 (14): L14703. Bibcode:2007GeoRL..3414703C. doi:10.1029/2007GL030207. S2CID 16596423.
  104. ^ Sunspot activity impacts on crop success New Scientist, 18 November 2004
  105. ^ "Sunspot activity may be linked to rainfall", New Scientist, 8 Nov., 2008, p. 10.
  106. ^ Forster, P.; V. Ramaswamy; P. Artaxo; T. Berntsen; R. Betts; D.W. Fahey; J. Haywood; J. Lean; D.C. Lowe; G. Myhre; J. Nganga; R. Prinn; G. Raga; M. Schulz; R. Van Dorland (2007), "Changes in Atmospheric Constituents and Radiative Forcing: § 2.9.1 Uncertainties in Radiative Forcing", in Solomon, S.; D. Qin; M. Manning; Z. Chen; M. Marquis; K.B. Averyt; M. Tignor; H.L. Miller (eds.), Contribution of Working Group I to the Fourth Assessment Report of the Intergovernmental Panel on Climate Change, 2007, Cambridge University Press, ISBN 978-0-521-88009-1
  107. ^ Molaverdikhani, Karan; Ajabshirizadeh, A. (2016). "Complexity of the Earth's space–atmosphere interaction region (SAIR) response to the solar flux at 10.7 cm as seen through the evaluation of five solar cycle two-line element (TLE) records". Advances in Space Research. 58 (6): 924–937. Bibcode:2016AdSpR..58..924M. doi:10.1016/j.asr.2016.05.035.
  108. ^ Hale, G. E.; Ellerman, F.; Nicholson, S. B.; Joy, A. H. (1919). "The Magnetic Polarity of Sun-Spots". The Astrophysical Journal. 49: 153. Bibcode:1919ApJ....49..153H. doi:10.1086/142452.
  109. ^ "NASA Satellites Capture Start of New Solar Cycle". PhysOrg. 4 January 2008. Retrieved 2009-07-10.
  110. ^ "Sun flips magnetic field". CNN. 16 February 2001. Archived from the original on 2005-11-15. Retrieved 2009-07-11.http://www.cnn.com/2001/TECH/space/02/16/sun.flips/index.html
  111. ^ Phillips, T. (15 February 2001). "The Sun Does a Flip". NASA. Archived from the original on 2001-11-04. Retrieved 2009-07-11.
  112. ^ Hazra, Soumitra; Nandy, Dibyendu (2016). "A Proposed Paradigm for Solar Activity Dynamics Mediated via Turbulent Pumping of Magnetic Flux in Babcock-Leighton-type Solar Dynamics". The Astrophysical Journal. 832 (1). 9. arXiv:1608.08167. doi:10.3847/0004-637X/832/1/9.
  113. ^ Yeates, Anthony R.; Nandy, Dibyendu; Mackay, Duncan H. (2008). "Exploring the Physical Basis of Solar Cycle Predictions: Flux Transport Dynamics and Persistence of Memory in Advection- versus Diffusion-dominated Solar Convection Zones". The Astrophysical Journal. 673 (1). 544. arXiv:0709.1046. Bibcode:2008ApJ...673..544Y. doi:10.1086/524352.
  114. ^ Karak, Bidya Binay; Nandy, Dibyendu (2012). "Turbulent Pumping of Magnetic Flux Reduxes Solar Cycle Memory and thus Impacts Predictability of the Sun's Activity". The Astrophysical Journal. 761 (1). L13. arXiv:1206.2106. Bibcode:2012ApJ...761L..13K. doi:10.1088/2041-8205/761/1/L13.
  115. ^ Muñoz-Jaramillo, Andrés; Dasi-Espuig, María; Balmaceda, Laura A.; DeLuca, Edward E. (2013). "Solar Cycle Propagation, Memory, and Prediction: Insights from a century of magnetic proxies". The Astrophysical Journal Letters. 767 (2). L25. arXiv:1304.3151. doi:10.1088/2041-8205/767/2/L25.
  116. ^ Route, Matthew (20 October 2016). "The Discovery of Solar-like Activity Cycles Beyond the End of the Main Sequence?". The Astrophysical Journal Letters. 830 (2): 27. arXiv:1609.07761. Bibcode:2016ApJ...830L..27R. doi:10.3847/2041-8205/830/2/L27. S2CID 119111063.
  117. ^ José Abreu; et al. (2012). "Is there a planetary influence on solar activity?" (PDF). Astronomy & Astrophysics. 548: A88. Bibcode:2012A&A...548A..88A. doi:10.1051/0004-6361/201219997.
  118. ^ S. Poluianov; I. Usoskin (2014). "Critical Analysis of a Hypothesis of the Planetary Tidal Influence on Solar Activity". Solar Physics. 289 (6): 2333. arXiv:1401.3547. Bibcode:2014SoPh..289.2333P. doi:10.1007/s11207-014-0475-0. S2CID 16188804.
  119. ^ F. Stefani; A. Giesecke; T. Weier (May 2019). "A Model of a Tidally Synchronized Solar Dynamo". Solar Physics. 294 (5): 60. arXiv:1803.08692. Bibcode:2019SoPh..294...60S. doi:10.1007/s11207-019-1447-1. S2CID 73609026.
  120. ^ K. Petrovay (2019). "Solar Cycle Prediction". Living Reviews in Solar Physics. 7: 6. doi:10.12942/lrsp-2010-6. PMC 4841181. PMID 27194963.
  121. ^ Cionco, Rodolfo G.; Kudryavtsev, Sergey M.; Soon, Willie W.-H. (May 2023). "Tidal Forcing on the Sun and the 11-Year Solar-Activity Cycle". Solar Physics. 298 (5): 70. arXiv:2304.14168. Bibcode:2023SoPh..298...70C. doi:10.1007/s11207-023-02167-w. S2CID 258352738.

General references

edit
edit
 
Wikimedia Commons has media related to Solar cycles.
Retrieved from "https://en.wikipedia.org/w/index.php?title=Solar_cycle&oldid=1246834273#History"