Tachocline

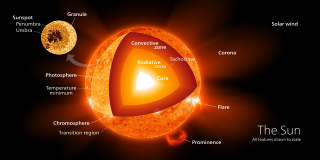
The tachocline is the transition region of stars of more than 0.3 solar masses, between the radiative interior and the differentially rotating outer convective zone. This causes the region to have a very large shear as the rotation rate changes very rapidly. The convective exterior rotates as a normal fluid with differential rotation with the poles rotating slowly and the equator rotating quickly. The radiative interior exhibits solid-body rotation, possibly due to a fossil field. The rotation rate through the interior is roughly equal to the rotation rate at mid-latitudes, i.e. in-between the rate at the slow poles and the fast equator. Recent results from helioseismology indicate that the tachocline is located at a radius of at most 0.70 times the solar radius (measured from the core, i.e., the surface is at 1 solar radius), with a thickness of 0.04 times the solar radius. This would mean the area has a very large shear profile that is one way that large scale magnetic fields can be formed.

Internal rotation in the Sun, showing differential rotation in the outer convective region (as a function of latitude) and almost uniform rotation in the central radiative region. The transition between these regions is called the tachocline. To convert the y-axis to period, use 500 nanoHz = 23.15 days.

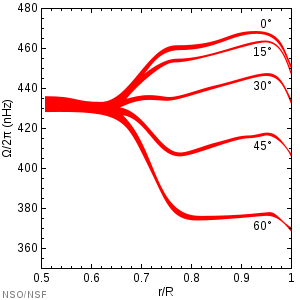
The geometry and width of the tachocline are thought to play an important role in models of the stellar dynamos by winding up the weaker poloidal field to create a much stronger toroidal field. Recent radio observations of cooler stars and brown dwarfs, which do not have a radiative core and only have a convective zone, demonstrate that they maintain large-scale, solar-strength magnetic fields and display solar-like activity despite the absence of tachoclines. This suggests that the convective zone alone may be responsible for the function of the solar dynamo.

The term tachocline was coined in a paper by Edward Spiegel and Jean-Paul Zahn in 1992 by analogy to the oceanic thermocline.

An illustration of the structure of the Sun

• Granules
• Sunspot
• Photosphere
• Chromosphere
• Convection zone
• Radiative zone
• Tachocline
• Solar core
• Solar corona
• Flare
• Prominence
• Solar wind

Additional References

• Miesch, Mark S. (2005). "Large-Scale Dynamics of the Convection Zone and Tachocline". Living Reviews in Solar Physics. 2 (1): 1. Bibcode:2005LRSP....2....1M. doi:10.12942/lrsp-2005-1. ISSN 1614-4961.
• Charbonneau, P.; Christensen-Dalsgaard, J.; Henning, R.; Larsen, R. M.; Schou, J.; Thompson, M. J.; Tomczyk, S. (December 1999). "Helioseismic Constraints on the Structure of the Solar Tachocline". The Astrophysical Journal. 527 (1): 445–460. Bibcode:1999ApJ...527..445C. doi:10.1086/308050. ISSN 0004-637X.
• Basu, Sarbani; Antia, H. M.; Narasimha, D. (March 1994). "Helioseismic measurement of the extent of overshoot below the solar convection zone". Monthly Notices of the Royal Astronomical Society. 267 (1): 209–224. Bibcode:1994MNRAS.267..209B. doi:10.1093/mnras/267.1.209. ISSN 0035-8711.
• Hughes, D. W.; Rosner, R.; Weiss, N. O. (2007-05-31). The Solar Tachocline. Cambridge University Press. p. 382. ISBN 978-1-139-46258-7.