Pompeiu's theorem is a result of plane geometry, discovered by the Romanian mathematician Dimitrie Pompeiu. The theorem is simple, but not classical. It states the following:
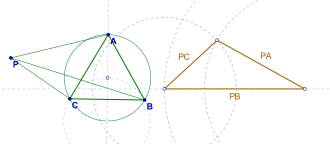

- Given an equilateral triangle ABC in the plane, and a point P in the plane of the triangle ABC, the lengths PA, PB, and PC form the sides of a (maybe, degenerate) triangle.[1][2]

The proof is quick. Consider a rotation of 60° about the point B. Assume A maps to C, and P maps to P '. Then , and . Hence triangle PBP ' is equilateral and . Then . Thus, triangle PCP ' has sides equal to PA, PB, and PC and the proof by construction is complete (see drawing).[1]
Further investigations reveal that if P is not in the interior of the triangle, but rather on the circumcircle, then PA, PB, PC form a degenerate triangle, with the largest being equal to the sum of the others; this observation is also known as Van Schooten's theorem.[1]
Generally, by the point P and the lengths to the vertices of the equilateral triangle - PA, PB, and PC two equilateral triangles ( the larger and the smaller) with sides and are defined:
- .
The symbol △ denotes the area of the triangle whose sides have lengths PA, PB, PC.[3]
Pompeiu published the theorem in 1936; however August Ferdinand Möbius had already published a more general theorem about four points in the Euclidean plane in 1852. In this paper Möbius also derived the statement of Pompeiu's theorem explicitly as a special case of his more general theorem. For this reason, the theorem is also known as the Möbius-Pompeiu theorem.[4]
External links
edit- MathWorld's page on Pompeiu's Theorem
- Pompeiu's theorem at cut-the-knot.org
Notes
edit- ^ a b c Jozsef Sandor: On the Geometry of Equilateral Triangles. Forum Geometricorum, Volume 5 (2005), pp. 107–117
- ^ Titu Andreescu, Razvan Gelca: Mathematical Olympiad Challenges. Springer, 2008, ISBN 9780817646110, pp. 4-5
- ^ Mamuka Meskhishvili: Two Non-Congruent Regular Polygons Having Vertices at the Same Distances from the Point. International Journal of Geometry, Volume 12 (2023), pp. 35–45
- ^ D. MITRINOVIĆ, J. PEČARIĆ, J., V. VOLENEC: History, Variations and Generalizations of the Möbius-Neuberg theorem and the Möbius-Ponpeiu. Bulletin Mathématique De La Société Des Sciences Mathématiques De La République Socialiste De Roumanie, 31 (79), no. 1, 1987, pp. 25–38 (JSTOR)







