User:Ahalda/aberration

Not to be confused with optical aberration.

The apparent position of a star viewed from the Earth depends on the Earth's velocity. The effect is typically much smaller than illustrated.

The aberration of light (also referred to as astronomical aberration or stellar aberration) is a relativistic phenomenon which causes objects to appear displaced to observers in motion. It is notable in astronomy for causing an apparent motion of stars and other celestial objects about their locations in the sky. It was historically influential in the development of the theories of heliocentrism, light, luminiferous aether, and Special Relativity.

Aberration causes objects to appear displaced towards the direction of the observer's motion by an angle of approximately v/c (in radians), where c is the speed of light and v is the observer's velocity. It occurs for much the same reason that falling rain appears to come from ahead to observers in a moving vehicle. Aberration's main astronomical consequence is "annual" aberration, which causes stars viewed from the Earth to appear to move in the sky over the course of a year in small ellipses with an angular radius of approximately 20 arcseconds, due to the finite speed of light relative to motion of the Earth as it revolves around the Sun.

Aberration was first observed around 1680 by a number of astronomers including Robert Hooke and John Flamsteed, who were instead searching for stellar parallax, but it was misunderstood for many years. James Bradley was the first scientist to understand it classically in 1729, and his theory and astronomical observations of aberration provided the first empirical proof of heliocentrism, convinced the scientific world that the speed of light is finite, and allowed him to make one of the earliest measurements of the speed of light.

In the 19th century aberration paved the way to the theory of Special Relativity. Thomas Young theorized that aberration implied the existence of an "aether wind" in 1804, and François Arago attempted to measure variations in the speed of light using aberration in 1810, but did not detect any. These observations were the main motivation for the aether drag theories of Augustin Fresnel (in 1818) and G. G. Stokes (in 1845), which, in combination with with new experiments and theory, led to Hendrick Lorentz' electromagnetic aether theory in 1892. Based on Lorentz' theory and on other observations, Albert Einstein then developed the theory of Special Relativity in 1905, and said that aberration was one of the experimental results which most influenced him.

Physical Origin

Light rays striking the earth in the Sun's rest frame compared to the same rays in the Earth's rest frame according to Special Relativity. The effect is exaggerated for illustrative purposes.

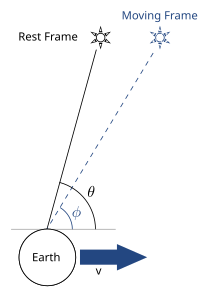
Aberration is the apparent change in angle of a beam of light due to a change in velocity of the oberver's frame of reference. It is frequently compared to the tilt of falling rain apparent to a moving observer: Rain that falls vertically will appear angled to moving observers, and they will want to carry umbrellas tilted slightly toward their direction of motion. The faster the observer moves, the more tilt is required. In the same way, a beam of light falling vertically will appear tilted to a moving observer, although the tilt is much smaller because the speed of light is much larger.

Aberration causes light beams striking a stationary observer from the sides to come angled from ahead in the observer's frame if the observer starts moving forwards. In the case of annual aberration of starlight, the direction of incoming starlight as seen in the Earth's instantaneous rest frame is tilted relative to the angle observed in the Sun's (approximately) inertial rest frame. Since the direction of motion of the Earth changes during its orbit, the direction of this tilting changes during the course of the year, causing the apparent position of the star to vary.

The difference in angle of light in a moving frame compared to a stationary frame is known as the angle of aberration, and can be computed classically and relativistically using the principle of velocity addition. While the classical reasoning gives intuition for aberration, it is inconsistent with certain observations even at the classical level (see history). The theory of Special Relativity correctly accounts for aberration.

Trigonometric relationships in the classical derivation of the angle of aberration, showing the change in angle of light in different frames.

Classical Derivation of the Angle of Aberration

In the Sun's frame, consider a beam of light moving at the speed of light $c$, with x and y velocity components $u_{x}$ and $u_{y}$, at an angle $\tan(\theta )=u_{y}/u_{x}$. If the Earth is moving at velocity $v$ in the x direction relative to the Sun, then by velocity addition the x component of the beam's velocity in the Earth's frame of reference is $u_{x}'=u_{x}+v$, and the y velocity is unchanged, $u_{y}'=u_{y}$. Thus the angle of the light in the Earth's frame $\phi$ in terms of the angle in the Sun's frame $\theta$ is

$\tan(\phi )={\frac {u_{y}'}{u_{x}'}}={\frac {u_{y}}{(u_{x}+v)}}={\frac {\sin(\theta )}{(v/c+\cos(\theta ))}}$

In the case of $\theta =90^{\circ }$, this result reduces to $\tan(\theta -\phi )=v/c$, and in the limit that v is much less than c the angle of aberration may then be approximated by $\theta -\phi =v/c$.

Relativistic Derivation of the Angle of Aberration

In Special Relativity the relativistic velocity addition formulae are used instead of classical velocity addition. Following the same logic as in the classical case, one then finds

$\tan(\phi )={\frac {\sin(\theta )}{\gamma (v/c+\cos(\theta ))}},\quad {\text{where}}\quad \gamma =1/{\sqrt {1-v^{2}/c^{2}}}$.

In the case of $\theta =90^{\circ }$, this equation reduces to $\sin(\theta -\phi )=v/c$, and in the limit that v is much less than c the angle of aberration may again be approximated by $\theta -\phi =v/c$. This relativistic formula keeps the speed of light ${\sqrt {u_{x}^{2}+u_{y}^{2}}}=c$ constant in all frames of reference as required by Special Relativity, and unlike the classical formula above.

The angle aberration may alternately, and more thoroughly, be derived by treating light as an electromagnetic wave. The angle of aberration can then be determined from Lorentz transformations of the electric and magnetic fields, giving the same result. This is how Albert Einstein derived the angle of aberration in his 1905 paper on Special Relativity, and this derivation properly accounts for the wave nature of light. Another result of this more careful electromagnetic derivation is the relativistic Doppler effect, which is a change in the frequency of light in different frames of reference. Thus, the Doppler effect and aberration are two aspects of the same relativistic phenomenon.

A light beam travels from a source to an observer in two different inertial frames of reference, showing that from the source's frame the tilting of the beam is best explained as aberration, while in the observer's frame it is a light-time correction. Click the image for a more detailed description.

Relationship to Light-Time Correction and Relativistic Beaming

Aberration is also equivalent two other phenomena, light-time correction, which is a correction to the measured position of an object due to its motion during the time taken by its light to reach an observer, and relativistic beaming, which is an angling of the light emitted by a moving light source. This relationship has been common source of confusion. Aberration is due to the motion of the observer, while light-time correction and relativistic beaming are due to the motion of the light source. Since velocities are relative, aberration in one inertial frame of reference is equivalent to a light-time correction in another frame of reference.

Note, however, that if the observer's frame is non-inertial this equivalence does not hold. For example, because the Earth is not an inertial frame but experiences centripetal acceleration towards the Sun, many aberrational effects such as annual aberration cannot be simply explained as light-time corrections in another frame. However, if the observer's velocity does not vary much during the light's time-of-flight, the observer's frame may be approximated as inertial and aberrational effects are equivalent to light-time corrections.

Astronomical Effects

Aberration causes a number of types of apparent motion in astronomy, each caused by different components of the Earth's motion:

• Annual aberration is due to the revolution of the Earth around the Sun.
• Diurnal aberration is due to the rotation of the Earth about its own axis.
• Secular aberration is due to the rotation of the Sun and solar system around the center of the galaxy.
• Planetary aberration is the combination of aberration and light-time correction.
• Stellar aberration is the combination of annual, diurnal and secular aberration.

Annual aberration

Aberration causes stars at the ecliptic poles appear to move in circles, stars exactly in the ecliptic plane move in lines, and stars at intermediate ecliptic latitudes move in ellipses. Shown here are the apparent motions of stars in these cases, and with ecliptic longitude of 270 degrees.

The direction of aberration of a star at the northern ecliptic pole differs over the course of a year.

Annual aberration is caused by the motion of an observer on the Earth revolving around the Sun, and typically causes each star to appear to move in a small ellipse over the course of a year. The major radius of the ellipse is equal to a value known as the constant of aberration, conventionally represented by $\kappa$, which represents the maximal angular displacement of a star due to annual aberration and may be calculated using the relation $\kappa =\theta -\phi \approx v/c$ substituting the Earth's average speed $v$ in the Sun's frame and the speed of light $c$. Its accepted value is 20.49552 arcseconds (at J2000).

Approximating the Earth's orbit as circular, annual aberration causes stars exactly on the ecliptic (the plane of the Earth's orbit) to appear to move back and forth along a straight line varying by $\kappa$ on either side of their average position. A star that is exactly at one of the ecliptic poles (at 90 degrees from the ecliptic plane) will appear to move in a circle of radius $\kappa$ about its average position, and stars at intermediate ecliptic latitudes will appear to move along small ellipses.

A star at the northern ecliptic pole, such as the star Polaris, is displaced in different directions at different times of the year when viewed by an observer on the 'top' of the Earth at a point on the arctic circle. At the time of the March equinox, the Earth's orbit carries the observer in a southwards direction, and the star's apparent declination is therefore displaced to the south by an angle of $\kappa$. At the September equinox, the star's position is displaced to the north by an equal and opposite amount. At the June and December solstices, the displacement in declination is zero. Conversely, the amount of displacement in right ascension is zero at either equinox and maximum at the solstices.

In practice the Earth's orbit is slightly elliptic rather than circular and its speed changes somewhat over the course of its orbit. Annual aberration is more accurately calculated using the Earth's instantaneous velocity relative to the barycenter of the Solar System.

Solar annual aberration

A special case of annual aberration is the nearly constant deflection of the Sun from its position in the Sun's rest frame by an angle $\kappa$ towards the west (as viewed from Earth), along the ecliptic. This deflection may equivalently be described as a light-time correction due to the motion of the Earth during the 8.3 minutes that it takes light to travel from the Sun to Earth, since the Earth's frame may be approximated as inertial during this short time. A simple geometrical light-time argument gives the same angular correction as found using aberration.

Diurnal and Orbital aberration

Diurnal aberration is caused by the velocity of the observer on the surface of the rotating Earth. It is therefore dependent not only on the time of the observation, but also the latitude and longitude of the observer. Its effect is much smaller than that of annual aberration, and is 0.32 arcseconds in the case of an observer at the equator where the rotational velocity is greatest. In the case of a satellite orbiting the Earth, the corresponding effect due to the orbital velocity of the satellite is known as orbital aberration.

Secular aberration

Secular aberration is due the revolution of the Solar System around the center of the Galaxy and affects the apparent positions of distant stars and extragalactic objects. However, since the galactic year is about 230 million years the aberration varies very slowly and the change in angle of aberration is extremely difficult to observe. Therefore secular aberration is usually ignored when considering the positions of stars. In other words, star maps show the observed apparent positions of the stars, not their calculated true positions in the Earth's frame after accounting for secular aberration.

Secular aberration causes a maximum displacement of 150 arcseconds (2.5 arcminutes), for example the stationary star Groombridge 1830 is displaced by approximately 3 arcminutes due to the combination of secular aberration and light-time correction. This is roughly 8 times the effect of annual aberration, since the velocity of the Solar System relative to the Milky Way is about 8 times the velocity of the Earth relative to the Sun.

For stars significantly less than 230 million light years away, the Solar System may be approximated as an inertial frame and so the effect of secular aberration is equivalent to a light-time correction. This includes stars in the Milky Way,which is about 100,000 light years in diameter. For these stars the position of the star in the galaxy's rest frame is easily computed from the product of its proper motion (in arcseconds per year) and its distance (in light years).

Planetary aberration

Planetary aberration is the combination of the aberration of light (due to the observer's velocity) and light-time correction (due to the object's motion and distance), as calculated in the rest frame of the Solar System. It is so called because it is usually applied to planets and other objects in the Solar System whose motion and distance are accurately known.

Stellar Abberation

Stellar aberration is the total aberration of a distant star due to all types motion of the observer on Earth. It is the combination of annual, diurnal and secular aberration. Annual aberration is the main contribution, since diurnal aberration is a much smaller effect and secular aberration is typically ignored due to its slow variation.

Applications

Aberration must be taken into account in many applications of astrometry.

Aberration was used in the Gravity_Probe_B experiment in order to measure the orientation of a satellite. The satellite tracked the apparent position of a star and fit this motion to the predicted apparent motion resulting from orbital and annual aberration. This measure of the satellite's orientation was then compared to the orientation of a set of gyroscopes, to measure the effect of gravity on the gyroscopes.

Hipparcos

doppler and terrell effect?

Poynting–Robertson effect

Sailing faster than the wind

Mason dixon line.

History

Search for Stellar Parallax

See also: Stellar parallax

TODO:

Aberration was first discovered as a result of attempts to measure stellar parallax in order to prove the theory of heliocentrism. The Nicolaus Copernicus' heliocentric theory of the solar system – that the Earth revolved annually about the Sun – had received confirmation by the observations of Galileo and Tycho Brahe and the mathematical investigations of Kepler and Newton.

As early as 1573, Thomas Digges had suggested that stellar parallax should occur according to the heliocentric model of the Solar System, and consequently if such parallaxes could be observed they would help confirm the heliocentric theory. Many observers claimed to have determined such parallaxes, but Tycho Brahe and Giovanni Battista Riccioli concluded that they existed only in the minds of the observers, and were due to instrumental and personal errors. In 1680 Jean Picard, in his Voyage d’Uranibourg, stated, as a result of ten years' observations, that Polaris, or the Pole Star, exhibited variations in its position amounting to 40″ annually. John Flamsteed, from measurements made in 1689 and succeeding years with his mural quadrant, similarly concluded that the declination of the Pole Star was 40″ less in July than in September. Robert Hooke, in 1674, published his observations of γ Draconis, a star of magnitude 2^m which passes practically overhead at the latitude of London, and whose observations are therefore free from the complex corrections due to astronomical refraction, and concluded that this star was 23″ more northerly in July than in October.

Hook and Flamsteed both thought that they were observing parralax, but these attempts were futile because the displacement due to aberration is orthogonal to any apparent displacement due to [stellar parallax]]. The maximum displacement south due to parallax occurs in December, while for aberration it occurs in March. Early astronomers searching for parallax were mystified by this apparently anomalous motion. Aberration is also now known to be a much larger effect: The highest displacement due to parallax is 0.76 arcseconds, for the star Alpha Centauri.

James Bradley

Bradley's data on the north-south component of the aberration of γ-Draconis in 1727 establishing stellar aberration.

James Bradley's Observations

In 1725, senior astronomer Samuel Molyneux, his junior partner and expert in precise astronomical measurements James Bradley, and clockmaker and scientific-instrument maker George Graham decided to reinvestigate the motion of γ Draconis in order to conclusively resolve the parallax question. Graham constructed a state-of-the-art zenith telescope at Molyneux's house in Kew, and the group began observations in December.

Bradley's measurements were of such an extraordinary accuracy and precision that he is regarded as having transformed astronomy into an exact science. Bradley's measurements were of an unprecedented six-figure accuracy of about 0.5 arcseconds, over a hundred times more accurate than previous astronomers', and he was the first astronomer to carefully control for sources of error by recording temperature and barometric pressure whenever he made an observation. He meticulously monitored and calibrated his telescope and apparatus, for example x. Friedrich Bessel, who later reanalyzed Bradley's data in light of more modern theory in 1810, called Bradley's control of error "incomparable". (Need something here about how Bessel found parallax, and is the one who continued/strengthened precision science based on Bradley's work. Physicist Freeman Dyson has argued that Bradley is "the inventor of modern science" because of his novel and influential understanding of the importance of error analysis.

Bradley observed that γ Draconis moved 40 arcseconds southwards between September and March, reversing its course from March to September. This motion was evidently not due to parallax nor was it due to observational errors, and Bradley commented that Hooke's conclusions were "really very far from being either exact or agreeable to the phenomena."

Hypotheses of Nutation and Atmospheric Refraction

Bradley and Molyneux first hypothesized that the apparent motion was due to a variation in the tilt of the axis of rotation of the Earth. They had already taken into account the slow precession of the Earth's axis, an effect known since ancient times, but now considered another possibility known as nutation, which causes smaller more rapid oscillations of the Earth's axis, which had been predicted by Isaac Newton. By this theory, the apparent position of stars on opposite sides of the celestial sphere would be displaced by an equal and opposite amount. Bradley proceeded to test this using a star with a right ascension nearly exactly opposite to that of γ Draconis, 35 Camelopardalis, but found its motion was inconsistent with this hypothesis. However, Bradley's observations were precise enough that he was later able observe a much smaller component of stellar motion consistent with nutation, for which he is credited with the discovery of the nutation of the Earth.

They also investigated the possibility that the motion was due to an irregular distribution of the Earth's atmosphere, thus involving variations in the index of refraction of the atmosphere over the course of the year, but again obtained negative results. Through this work Bradley developed a model of atmospheric refraction and high precision numerical tables which were used for the next century for navigation and surveyal purposes.

Bradley's Classical Explanation

On August 19, 1727, Bradley then embarked upon a further series of observations using a telescope of his own erected in Wanstead. This instrument had the advantage of a larger field of view and he was able to obtain precise positions of 200 stars over the course of about two years. This established the existence of the phenomenon of aberration beyond all doubt, and allowed Bradley to observe that the apparent motion followed a general law that applied to all stars.

Bradley developed the explanation of aberration in about September 1728 and his theory was presented to the Royal Society in mid January the next year. One well-known story is that he came to this explanation after he saw the change of direction of a wind vane on a boat on the Thames, caused not by an alteration of the wind itself, but by a change of course of the boat relative to the wind direction. However, Bradley did not record this incident in his account of the discovery, and it may therefore be apocryphal.

As light propagates down the telescope, the telescope moves requiring a tilt to the telescope that depends on the speed of light. The apparent angle of the star φ differs from its 'rest' angle θ

Bradley explained aberration in terms of a corpuscular theory of light in which light is made of small billiard-ball-like particles unaffected by gravity, as was generally accepted at the time. His classical explanation appeals to the motion of the Earth relative to a beam of light-particles moving at a finite velocity, and is developed in the Sun's frame of reference, unlike the classical derivation given above.

Bradley reasoned as follows: Consider a distant star, motionless relative to the Sun and extremely far away so that parallax may be ignored. Suppose the star is observed on Earth with a telescope, idealized as a narrow tube. The light enters the tube from the star at angle $\theta$ and travels at finite speed $c$ taking a time $h/c$ to reach the bottom of the tube, where it is detected. If the Earth is moving with a speed $v$, then during the transit of the light the tube moves a distance $vt=vh/c$. Consequently, for the particles of light to reach the bottom of the tube, the tube must be inclined at an angle $\phi$ different from $\theta$, resulting in an apparent position of the star at angle $\phi$, as illustrated in the figure to the side. The apparent angle and true angle are related using trigonometry as:

$\tan(\phi )={\frac {h\sin(\theta )}{hv/c+h\cos(\theta )}}={\frac {\sin(\theta )}{v/c+\cos(\theta )}}$.

The impact of Bradley's discoveries

This result allowed Bradley to make one of the earliest measurements of the speed of light. He measured it to be 301,000 m/s, within one percent of the modern value of 299,792.458 m/s. (need to talk about how he only measured the ration v/c, and only quoted the time-of-flight of light from the sun to earth as 8.12 min, and also need to refer to other measurements of the astronomical unit, which was measured by that time and could be used to measure the speed of light.)

“These different methods of finding the velocity of light thus agreeing in the result, we may reasonably conclude, not only that these phænomena are owing to the causes to which they have been ascribed; but also, that light is propagated (in the same medium) with the same velocity after it hath been reflected as before.”52 And so there was a confirmation of a finite speed of light, made possible by the disjointedness in approach of two determinations, and their eventual near agreement for the value of the speed. (prof of finite speed of light) (proof of heliocentric theory) (mention that bradley confirmed Newton's estimate of the distance of stars) (constancy of the speed of starlight)

Bradley's discoveries of aberration and the nutation of the Earth were called "the most brilliant and useful of the century" by Jean Baptiste Joseph Delambre, historian of astronomy and mathematical astronomer, in his history of astronomy in the 18th century (1821).[1] Pierre-Simon Laplace, in his overview of physics "Exposition du système du monde" (1813) similarly commented that "Bradley, the model astronomer, is forever famous because of two of the most beautiful discoveries ever made in astronomy, the aberration of the fixed stars, and the nutation of the Earth's axis."

Halley remarked that "three Grand Doctrines in the Modern Astronomy do receive Great Light and Confirmation from this one Single Motion of the Stars Vizt. The Motion of the Earth, the Motion of Light and the immense distance of the Stars"

Paragraph about charles mason and the mason dixon line here.

Thomas Young

Young reasoned that aberration could only be explained if the aether was immobile in the frame of the Sun. Here, a pulse of light is transmitted to a telescope. On the left, stellar aberration occurs if an immobile aether is assumed, showing that the telescope must be tilted. On the right, the aberration disappears if the aether moves with the telescope, and the telescope does not need to be tilted.

The Wave Theory of Light

See also: Luminiferous aether and Wave Theory of Light

Later in the 18th century aberration influenced the development of the wave theory of light, which was a competing theory to Newton's corpuscular (or emission) theory of light, and which is the basis for the modern theory of light. In its early form the wave theory postulated that light is a wave propagating through a fluid medium known as the luminiferous aether, much like sound waves propagate through air.

Although the wave theory is more correct, the corpuscular theory was dominant through the 18th and early 19th century and aberration was considered by some to be strong evidence in its favor. As early as 1737, Clairaut had commented that aberration provided strong evidence for Newton's theory. Laplace wrote in his Exposition du système du monde in 1813 that "The phenomena of double refraction and the aberration of the stars appear to me to give to the emission theory or light, if not complete certainty, at least an extreme probability. These phenomena are inexplicable under the hypothesis of undulations of a fluid ether." (should discuss how paradoxically, aberration is much easier to explain in the emmision theory, according to darrigol)

Leonard Euler, a prominent defender of wave theory in the 18th century, remarked in 1746 that aberration could be equally well explained within wave theory as it is merely the consequence of the vector addition of velocities. However, his theory did not gain much attention.

Aether Wind

Much later, in the early 19th century Thomas Young pioneered the revival of the wave theory of light, and following Euler he found aberration could be explained within wave theory. However, he also realized aberration had an important implication for the nature of the luminiferous aether: The aether must immobile in the Sun's reference frame and must pass through the Earth unaffected, since if the aether moved along with the Earth the light would move with it and no aberration would be observed. In 1804 he wrote "Upon consideration of the phenomena of the aberration of the stars I am disposed to believe that the luminiferous aether pervades the substance of all material bodies with little or no resistance, as freely perhaps as the wind passes through a grove of trees."

Augustin Fresnel, another 19th century pioneer of wave theory whose numerous discoveries led to its eventual acceptance and the obsolescence of emission theory, independently came to the same conclusion as Young of an aether wind around 1815, although he never published it because of Young's priority. Aberration was the first subject he ever considered in wave theory, and it may have had a significant impact on his thoughts on wave theory and on the nature of the luminiferous aether.

Once the wave theory was accepted, the existence of this "aether wind" became a major point of contention for almost a century, and many scientists found it difficult to accept on aesthetic grounds. It became a major driving force behind the developments that eventually led to the theory of Special Relativity.

First Evidence of Special Relativity

Aberration opened a new avenue of research in the early 19th century as a result of experimental observations which were inexplicable by the classical theories of light. Both Bradley and Young's theories predict that the angle of aberration depends on the velocity of light c, which at the time was thought to vary, causing variations in the angle of aberration. However, no such variations could be observed. This is now known to be a consequence of Special Relativity, which holds that the speed of light is constant in all frames of reference.

One such experiment is the water telescope, first discussed by the astronomer Ruđer Bošković in 1766. Although this experiment was not performed until much later, it was an influential thought experiment. The velocity of the light in a telescope filled with water will be slower than in vacuum in both Bradley and Young's theories, and is given by $c/n$ rather than $c$, where $n$ is the index of refraction of the water. Substituting this speed in the formula for the angle of aberration shows there will be a medium-dependent angle of aberration. However, in 1782 the water telescope was reanalyzed Patrick Wilson who argued that Bošković had forgotten to account for refraction at the telescope's objective, which negated the dependence. Other scientists were uncertain, and because of this the experiment was not performed until much later Hoek in 1842 and most precisely by Airy in 1871, once aberration had become a significant issue in electromagnetic theory. The angle of aberration is observed to be unaffected by the medium in the telescope.

In 1810 François Arago was unsatisfied with Bošković and Wilson's treatment and performed a different test based on a prediction of corpuscular theory, and his result is sometimes considered to be the first experimental evidence of Special Relativity. Astronomers such as John Michell believed that (in corpuscular theory) the velocity of incoming starlight would depend on the velocity and mass of each star, which would cause small variations in the angle of aberration among stars. Bradley had already thought of this and found no such variation, leading him to conclude that all starlight had the same velocity, but other astronomers argued the variance in angle was simply too small for Bradley to detect. Arago realized he could more precisely test this by placing a prism at the end of the telescope, since in the classical theories light beams of different velocities would refract by different, readily measurable, amounts. With the prism Arago could also measure the annual variation of the velocity of starlight in the Earth's frame predicted by both the corpuscular and wavelike theories. However, Arago observed no such variations, a result inexplicable by the classical theories, which he struggled to explain. Arago initially hypothesized the human eye could only see light of one particular velocity, while stars shone light of many velocities. Thus, a person would only see the component of starlight which had suitable velocity in the Earth's instantaneous frame, which would therefore always refract by the same amount. However, this was unsatisfactory.

Aether Drag Models

See also: Aether drag hypothesis

Fresnel's Aether Drag

Although Augustin Fresnel had abanoned his earlier studies of aberration, they had led him to contact Arago, who then became his mentor. Following Fresnel's great progress with the wave theory of light, which he successfully used to explain diffraction, birefringence, and polarization, Arago asked him to examine the still unexplained refractive aberration experiments. In 1818 Fresnel developed an aether theory known as the aether drag hypothesis to explain them.

Fresnel suggested that the aether is generally at rest in the Sun's frame of reference (as both Young and Fresnel had thought before) but that the aether is fluid and objects partially drag the aether along with them as they move through it. That is, the aether in an object of index of refraction $n$ moving at velocity $v$ is partially dragged with a velocity $(1-1/n^{2})v$ bringing the light along with it. This factor is known as "Fresnel's dragging coefficient". This dragging effect, along with refraction at the telescope's objective, compensates for the slower speed of light in the water telescope in Bradley's explanation. With this modification Fresnel obtained Bradley's vacuum result even for non-vacuum telescopes, and was also able to predict many other phenomena related to the propagation of light in moving bodies.

Note that the speed of light still varies in the Earth's frame in Fresnel's theory. Rather than attributing Arago's aberration result to the constancy of the speed of light, he attributed it to properties of moving refractive bodies. Also note that the aether wind still exists in Fresnel's theory.

(some note on the influence of Fresnel's theory)

Conceptual illustration of Stokes' aether drag theory. In the rest frame of the Sun the Earth moves to the right through the aether, in which it induces a local current. A ray of light (in red) coming from the vertical becomes dragged and tilted due to the flow of aether.

Stokes' Aether Drag

The fact that light is polarized led Fresnel himself to develop the idea that aether was an elastic solid, since only such a solid supports the transverse vibrations required for polarized waves. Scientists such as Cauchy and Green further developed this theory and came to believe that the aether was a totally immobile elastic solid as opposed to Fresnel's original fluid aether. There was thus renewed need for an explanation of aberration consistent both with Fresnel's predictions (and Arago's observations) as well as polarization.

In 1845 Sir George Stokes applied his knowledge of fluid mechanics to the problem, and proposed a 'putty-like' aether which acts as a liquid on large scales but as a solid on small scales, thus supporting both the transverse vibrations required for polarized light and the fluidity required to explain aberration. Making only the assumptions that the fluid is irrotational and that the boundary conditions of the flow are such that the aether has zero velocity far from the Earth but moves at the Earth's velocity at its surface and within it, he was able to account for aberration and derive the angle of aberration v/c. The velocity of the aether outside of the Earth would decrease as a function of distance from the Earth so light rays from stars would be progressively dragged as they approached the surface of the Earth. No variation in the angle of aberration would be detected in Arago's prism or the water telescope because the light would be "fully" dragged by the aether within the telescope, in contrast to Fresnel's "partial" dragging.

Electromagnetism

During much of the second half of the 19th century the focus of inquiry turned to the electromagnetic properties of light and aether, leading to the discovery that light is an electromagnetic wave. In the 1880s once electromagnetism was better understood, interest turned again to the problem of aberration and its implications for electromagnetic theory. By this time flaws were known to both Fresnel's and Stokes' theories. Fresnel's theory required that the relative velocity of aether and matter be different for light of different colors, because of the frequency dependence of indices of refraction of many media, and it was shown that the boundary conditions Stokes had assumed in his theory were inconsistent with his assumption of irrotational flow. Many scientists also disliked the aether drag theories on aesthetic grounds (add some quotes)

In addition, Fresnel and Stoke's aberration theories had inspired a new series of experiments, known as aether drift experiments and also often referred to as aberration experiments, testing the effect of the motion of the Earth and the aether on the propagation of light. These include the Fizeau experiment in x, the Michelson Morely experiment in x, . New electromagnetic theories had to explain these results in addition to aberration.

At the same time, the modern theories of electromagnetic aether could not account for aberration at all. Many scientists such as Maxwell, Heaviside, JJ Thomson and Hertz unsuccessfully attempted to solve these problems by incorporating either Fresnel or Stokes' theories into Maxwell's new electromagnetic laws. Lord Kevlin said of these attempts,

Fresnel and Stokes have done all that man has been able to do, to express the dynamics of the aberration of light. The aberration of light is still an absolute mystery.

— Lord Kelvin, 1889

Lorentz' Electromagnetic Theory

See also: Lorentz ether theory

Hendrik Lorentz spent considerable effort along these lines to develop an electromagnetic theory consistent with aberration and related observations. After working on this problem for a decade, the issues with Stokes' theory caused him to abandon it and to follow Fresnel's suggestion of a (mostly) stationary aether (1892, 1895). However, in Lorentz's model the aether was completely immobile, like the electromagnetic aethers of Cauchy, Green and Maxwell and unlike Fresnel's aether. He obtained Fresnel's dragging coefficient from modifications of Maxwell's electromagnetic theory, XXX Poincare XXX including a modification of the time coordinates in moving frames ("local time"). In order to explain the Michelson-Morely experiment (1887), which apparently contradicted both Fresnel's and Lorentz's immobile aether theories, and apparently confirmed Stokes' complete aether drag, Lorentz theorized (1892) that objects undergo "length contraction" by a factor of ${\sqrt {1-v^{2}/c^{2}}}$ in the direction of their motion through the aether. In this way, aberration (and all related optical phenomena) can be accounted for in the context of an immobile aether. Lorentz' theory became the basis for much research in the next decade, and beyond. Its predictions for aberration are identical to those of the relativistic theory.

Special relativity

See also: History of special relativity

Lorentz' theory matched experiment well, but it was complicated and made many unsubstantiated physical assumptions about the microscopic nature of electromagnetic media. In his 1905 theory of Special Relativity, Albert Einstein reinterpreted the results of Lorentz' theory in a much simpler and more natural conceptual framework which disposed of the idea of an aether. His derivation is now the accepted explanation.

Robert S. Shankland reported some conversations with Einstein, in which Einstein emphasized the importance of aberration:

He continued to say the experimental results which had influenced him most were the observations of stellar aberration and Fizeau’s measurements on the speed of light in moving water. “They were enough,” he said.

Other important motivations for Einstein's development of relativity were the moving magnet and conductor problem and (indirectly) the negative aether drift experiments, already mentioned by him in the introduction of his first relativity paper. Einstein wrote in a note in 1952:

My direct path to the sp. th. rel. was mainly determined by the conviction that the electromotive force induced in a conductor moving in a magnetic field is nothing other than an electric field. But the result of Fizeau’s experiment and the phenomenon of aberration also guided me.

While Einstein's result is the same as Bradley's original equation except for an extra factor of $\gamma$, it should be emphasized that Bradley's result does not merely give the classical limit of the relativistic case, in the sense that it gives incorrect predictions even at low relative velocities. Bradley's explanation cannot account for situations such as the water telescope, nor for many other optical effects (such as interference) that might occur within the telescope. This is because in the Earth's frame it predicts that the direction of propagation of the light beam in the telescope is not normal to the wavefronts of the beam, in contradiction with Maxwell's theory of electromagnetism. It also does not preserve the speed of light c between frames. However, Bradley did correctly infer that the effect was due to relative velocities.

In the limit of small velocity of the observer, Einstein's result reduces to Fresnel's derivation of aberration.

Einstein put to rest the question which had arisen since hte earliest discoveries of aberration, of how it depended on the speed of light, by showin that the speed of light is constant. (A brief history of the speed of light before eisntein)

See also

• Aberration
• Nutation
• Proper motion
• Apparent place
• Fresnel, Augustin-Jean
• List of astronomical topics
• Stokes, George Gabriel
• Timeline of electromagnetism and classical optics
• Stellar aberration (derivation from Lorentz transformation)

References

• Stephen Peter Rigaud, Memoirs of Bradley (1832)
• Charles Hutton, Mathematical and Philosophical Dictionary (1795).
• H. H. Turner, Astronomical Discovery (1904).

External links

• Stellar Aberration at MathPages
• Courtney Seligman on Bradley's observations
• [1] "From Stargazers to Starships" by David P. Stern
• [2] "C-ship: The Aberration of Light" by John Walker at Fourmilab

Attribution

This article incorporates text from a publication now in the public domain: Chisholm, Hugh, ed. (1911). Encyclopædia Britannica (11th ed.). Cambridge University Press. {{cite encyclopedia}}: Missing or empty |title= (help)