The Newton-Gauss Line
In mathematics, the Newton-Gauss Line is a property of a theorem known as the Theorem of Complete Quadrilateral, which is a proof within the field of geometry. It is a geometric relation of properties, with a specific interest in the midpoints of line segments within a complete quadrilateral, also known as a tetragram. The theorem states that the midpoints of the three diagonals of a complete quadrilateral lie on a single line. This connecting line is referred to as the Newton-Gauss Line.
The Newton-Gauss Line is very similar to the Newton Line, which follows the same general theorem but uses a convex quadrilateral with at most two parallel sides; this also means instead of having three diagonals, it uses the midpoint of the two s in addition to the point which bisects two lines created by connecting the midpoints of the opposite sides of the quadrilateral.
Theorem of Complete Quadrilateral
editThe Theorem of Complete Quadrilateral states that any four lines that are in general position (no two lines are parallel, and no three are concurrent) defines a total of six points; the configuration of these six points, in addition to the line segments belonging to these given lines, are known as the complete quadrilateral. Additionally, a key property is that these 6 points can be split into pairs where their connecting segments do not lie on any of the given 4 lines. These line segments are called diagonals of the quadrilateral. When connecting the midpoints of these diagonals, this forms the Newton-Gauss Line.
Properties
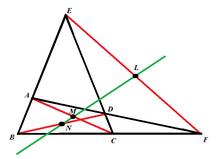
editA complete quadrilateral is the polygon determined by four lines, with there being no three lines that are concurrent, and their six points of intersection. A complete quadrilateral (figure 1) has three distinct diagonals: , , and . It should be noted that regular polygons only have two distinct diagonals. The midpoints of these diagonals; , , and , form a line when connected together - this is the Newton-Gauss Line.
One property that is interesting is the distance between the points that make up the Newton-Gauss Line. From the Newton Line, we can see that the outer points of the line are equidistant to the central point of the line. The Newton-Gauss Line does not follow the same equidistance between points. This is due to the extra two points in the complete quadrilateral being able to extend extremely far along the lines, only limited by the angles at which the inner points create.
Applications
editAlthough the Newton-Gauss Line's applications on a broader spectrum of mathematics is limited, the Newton-Gauss Line is a fundamental concept when dealing with complete quadrilaterals, used to develop an understanding of how quadrilaterals operate and can be manipulated when their vertices are modified. It is also used as a basis for being able to collect a plethora of other information used in the analysis of complete quadrilaterals.
The following are some possible applications of the complete quadrilaterals which are associated with cyclic quadrilaterals, based on the works presented by Barbu and Patrascu.
Angle Equality
editYou are able to show angular equality between points on the complete quadrilateral and points lying on the Newton-Gauss Line.
Given any cyclic quadrilateral , let point be the point of intersection between the two diagonals and . Extend out the diagonals and until they meet at a point of intersection and let this point be . Let the midpoint of the segment be , and let the midpoint of the segment be (Figure 1).
Theorem
editIf the midpoint of the segment is , the Newton-Gauss Line of the complete quadrilateral in addition to the line determines an equal to .
Proof
editFirst we must show that the triangles and are similar.
Since and additionally ,we know . Also,
Within the cyclic quadrilateral , we have the set of equalities
Therefore,
We let and be the radii of the circumcircles of and respectively. If we apply the law of sines to the triangles, we are given:
Since and also , we have shown the equality . The similarity of triangles and follows, and .
Remark
editIt should be noted that is is the midpoint of the line segment , by the same reasoning we can show that .
Angle Equality Parallel to the Newton-Gauss Line
editYou are able to draw additional parallel lines to the lines on the complete quadrilateral which connect to the Newton-Gauss Line. By doing this, you can also show that several angles are equal within the complete quadrilateral. (Figure 2)
Theorem
editThe parallel line from to the Newton-Gauss Line of the complete quadrilateral in addition to the line are isogonal lines of .
Proof
editSince we know from the proof conducted in the first application that triangles and are similar, we have the equality . We denote the point on intersection between the side with the parallel of through as the point .
Because we know and , we can show that , and additionally that .
Therefore, .
Two Cyclic Quadrilaterals
editYou are able to show that the points lying on the diagonals in combination with points that lie on the given 4 lines will form two cyclic quadrilaterals, and as a result, you are then able to prove that the two complete quadrilaterals contained within these have the same Newton-Gauss Line.
Theorem 1
editLet and be the orthogonal projections of the point on the lines and respectively.
The quadrilaterals and are cyclic.
Proof
editFrom the theorem presented in the Angle Equality application, we know that . The points and are the respective circumcenters of the right triangles and . It then follows with the assumption that and .
Therefore,
Therefore, we have shown that is a cyclic quadrilateral, and it's twin is also cyclic by the same reasoning.
Theorem 2
editExtend the lines and to intersect and at and respectively (Figure 4).
The complete quadrilaterals and have the same Newton-Gauss Line.
Proof
editThe two complete quadrilaterals have a shared diagonal, . When each complete quadrilateral's Newton-Gauss Line is calculated, it is found that lies on the Newton-Gauss Line of both quadrilaterals. It is worth noting that is equidistant from and , since it is the circumcenter of the cyclic quadrilateral .
We show that triangles and are congruent, and thus it follows that lies on the perpendicular bisector of the line . Therefore, the line contains the midpoint of , and is the Newton-Gauss Line of .
Now for us to show that the triangles and and are congruent, we must first note that since we have the points and being midpoints of and respectively, is a parallelogram.
From this, we can come to the conclusion that
- ,
- , and
- .
It is important to note that .
When we combine this with the third dot point above, we find:
.
Together, with the other two dot points above, this proves the congruence of triangles and .
Remark
editDue to and being congruent triangles, their circumcentres and are also congruent.
References
edit- Barbu, C. & Patrascu, I.: Some Properties of the Newton-Gauss Line
- Johnson, R.A.: Modern geometry; an elementary treatise on the geometry of the triangle and the circle.
- Bogomolny, A.: Theorem of Complete Quadrilateral
- Alperin, R.C.: Gauss-Newton Lines and Eleven Point Conics.
- Planet Math: Line Segments
