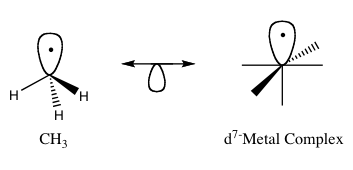
The isolobal principle (more formally known as the isolobal analogy) as developed by Roald Hoffman, is a strategy used in organometallic chemistry to relate the structure of organic and inorganic molecular fragments in order to predict bonding properties of organometallic compounds.[1] Hoffman described molecular fragments as isolobal “if the number, symmetry properties, approximate energy and shape of the frontier orbitals and the number of electrons in them are similar – not identical, but similar.” One can predict the bonding and reactivity of a lesser-known species from that of a better-known species if the two molecular fragments have similar frontier orbitals, the highest occupied molecular orbital, HOMO, and the lowest unoccupied molecular orbital, LUMO. When representing pairs of isolobal structures, their relationship is symbolized by:
For his work on the isolobal analogy, Roald Hoffman was awarded the Nobel Prize in Chemistry in 1981, which he shared with Kenichi Fukui. In his Nobel Prize lecture, Hoffman stressed that the isolobal analogy is a useful, yet simple, model and thus is bound to fail in certain instances.
Construction of Isolobal Fragments
editTo begin to generate an isolobal fragment, the molecule needs to follow certain criteria.[2] Molecules based around main group elements should satisfy the octet rule when all bonding and nonbonding molecular orbitals (MO) are filled and all antibonding MOs are empty. For example methane is a simple molecule from which to form a main group fragment. The removal of a hydrogen atom from methane generates a methyl radical. The molecule retains its molecular geometry as the frontier orbital points in the direction of the missing hydrogen atom. Further removal of hydrogen results in the formation of a second frontier orbital. This process can be repeated until only one bond remains to the molecules central atom. Figure 2 demonstrates this example of step-by-step generation of isolobal fragments.
The isolobal fragments of octahedral complexes, such as ML6, can be created in a similar fashion. Transition metal complexes should initially satisfy the eighteen electron rule, have no net charge, and their ligands should be two electron donors (Lewis bases). Consequently, the metal center for the ML6 starting point must be d6. Removal of a ligand is analogous to the removal of hydrogen of methane in the previous example resulting in a frontier orbital, which points toward the removed ligand. Cleaving the bond between the metal center and one ligand results in a ML5- radical complex. In order to satisfy the zero charge criteria the metal center must be changed. For example, a MoL6 complex is d6 and neutral. However, removing a ligand to form the first frontier orbital would result in a MoL5- complex because Mo has obtained an additional electron making it d7. To remedy this, Mo can be exchanged for Mn, which would from a neutral d7 complex in this case. This trend can continue until only one ligand is left coordinated to the metal center, as shown in Figure 3.
Relationship between tetrahedral and octahedral fragments
editIsolobal fragments of tetrahedral and octahedral molecules can be related. Structures with the same number of frontier orbitals are isolobal to one another. For example, the methane with two hydrogen atoms removed, CH2 is isolobal to a d8 ML4 complex formed from an octahedral starting complex (Figure 4). Similar analogies can be made between either CH3 and d7-ML5 or CH and d9-ML5.
MO Theory Dependence
editAny sort of saturated molecule can be the starting point for generating isolobal fragments.[3] [4] The molecules’ bonding and nonbonding MOs should be filled and the antibonding MOs empty. With each consecutive generation of a isolobal fragment, electrons are removed from the bonding orbitals and a frontier orbital is created. The frontier orbitals are at a higher energy level than the bonding and nonbonding MOs. Each frontier orbital contains one electron. For example, consider Figure 5, which shows the production of frontier orbitals in tetrahedral and octahedral molecules.
As seen above, when a fragment is formed from CH4, one of the sp3 hybrid orbitals involved in bonding becomes a nonbonding singly occupied frontier orbital. The frontier orbital’s increased energy level is also shown in the figure. Similarly when starting with a metal complex such as d6-ML6, the d2sp3 hybrid orbitals are affected. Furthermore the t2g nonbonding metal orbitals are unaltered.
Extensions of the Analogy
editThe isolobal analogy has applications beyond basic octahedral complexes. The analogy can be used with a variety of ligands, charged species and non-octahedral complexes.[5]
Ligands
editAs stated above, typical ligands used in the isolobal analogy are two-electron donors such as phosphines, halogens or carbonyls. However, other types of ligands can also be employed. If ligands donate multiple pairs of electrons, they will occupy multiple coordination sites. For example, cyclopentadiene is a six-electron donor that occupies three coordination sites. Polydentate ligands can also be used in the analogy, such as ethylenediamine, a bidentate ligand, or triethylenetetramine, a tetradentate ligand.
Isoelectronic Fragments
editThe isolobal analogy can also be used with isoelectronic fragments with the same coordination number. This allows for the inclusion of charged species in the analogy. For example, Re(CO)5 is isolobal with CH3 and therefore, Ru+(CO)5 and Mo-(CO)5 are also isolobal with CH3. Any 17-electron metal complex would be isolobal in this example.
In a similar sense, the addition or removal of electrons from two isolobal fragments results in two new isolobal fragments. Since Re(CO)5 is isolobal with CH3, Re(CO)5+ is isolobal with CH3+. [6]
Non-Octaherdral Complexes
editUntil this point only the tetrahedral and octahedral geometries have been used, but the analogy can also be applied to other shapes. The derivations from octahedral geometry is valid for most other geometries except square-planar because square-planar complexes typically abide to the 16-electron rule. Assuming ligands act as two-electron donors the metal center in square-planar molecules is d8. To relate an octahedral fragment, MLn, where M has a dx electron configuration to a square planar analogous fragment, the formula MLn-2 where M has a dx+2 electron configuration should be followed. Further example of the isolobal analogy in various shapes and forms are shown in Figure 8.
Applications and Examples
editUses of the isolobal analogy include providing a short-cut to understanding electronic structure, predicting reactivity and reaction mechanisms, and a method of classifying molecules. Applications are typically utilized to make connections between well-known systems and less familiar systems. For example, the possibility of unsynthesized compounds can be imagined from those of known molecular conformations. The isolobal analogy does not guarantee these products are capable of being produced, but only proposes a possibility. Consider the molecule Fe(CO)3 complexed with cyclobutadiene. [1] Fe(CO)3 is isolobal with CH+. Therefore one can predict that CH+ will coordinate with cyclobutadiene in a similar fashion that Fe(CO)3 will. Thus the molecule C5H5+ can be envisioned regardless of it’s actuality.
Predicting the reactivity of complexes can also be accomplished using the isolobal analogy. From the simple expectation of two CH3 radicals reacting to form ethane one can use the analogy to predict M-C or M-M bonding such as (CH3)M(CO)5 and M2(CO)10, where M is d7.
Another application of the isolobal analogy is assisting in predicting reaction mechanisms. As in the other applications the mechanisms of well-known reactions can be used to help predict mechanistic pathways of lesser-known reactions. There is no limit on the potential comparisons between organic and inorganic complexes. The analogy can flow in either direction (Organic to Inorganic) or within each division (Organic to Organic).
Arteaga-Muller et al. utilize the isolobal analogy to relate imido half-sandwhich complexes with isoelectronic dicyclopentadienyl complexes. [7] The isolobal relationship of the imido and the cyclopentadienyl ligands is the key to this comparison. The study found the reactivity of these two types of complexes to be similar although their catalytic abilities differed in some respects. This study shows that the isolobal analogy does not make perfect predictions between two isolobal fragments, as warned by Hoffman in his Nobel Lecture.
Wu et al. apply the isolobal analogy to explore relationships involving structures, energies and magnetic properties between polyhedral boron carbonyls and their hydrocarbon relatives.[8] As determined in this study, although isolobal, these two sets of molecules have significant differences in their strain energy.
Goldman and Tyler used the isolobal analogy to determine the most likely mechanism for a deletion reaction.[9] One of the products of the irradiation of CpW(CO)3Me in the presence of PPh3 is CpW(CO)3-. The mechanism of said reaction was studied and theorized to be isolobal to the disproportionation of metal-metal bonded dimers involving 19-valence electron intermediates. The reactions are composed of isolobal fragments and the key intermediates of both reactions are isolobal. Thus, the reaction pathways are mechanistically isolobal.
References
edit- ^ a b Roald Hoffmann (1982). "Building Bridges Between Inorganic and Organic Chemistry". Angewandte Chemie International Edition. 21 (10): 711–24. doi:10.1002/anie.198207113. Cite error: The named reference "Hoffman" was defined multiple times with different content (see the help page).
- ^ Department of Chemistry. Modern Approached to Inorganic Bonding. University of Hull.
- ^ Joan Ribas Gispert (2008). Coordination Chemistry. WILEY-VCH.
{{cite book}}: Text "pages172-176" ignored (help) - ^ Shriver, D.F.; Atkins, P.; Overton, T.; Rourke, J.; Weller, M.; Armstrong, F. (2006). Inorganic Chemistry. Freeman.
{{cite book}}: Cite has empty unknown parameter:|1=(help) - ^ Gary L. Miessler; Donald A. Tarr (2008). Inorganic Chemistry (3 ed.). Pearson Education, Inc.
- ^ Douglas, B.; McDaniel, D.; Alexander, J. (1994). Concepts and Models of Inorganic Chemistry (3 ed.). Wiley & Sons.
- ^ Arteaga-Müller, R.; Sánchez-Nieves, J.; Ramos, J.; Royo, P.; Mosquera, M.E.G. (2008). "Isolobal Zwitterionic Niobium and Tantalum Imido and Zirconium Monocyclopentadienyl Complexes: Theoretical and Methyl Methacrylate Polymerization Studies". Organometallics. 27: 1417–26. doi:10.1021/om701068h.
- ^ Wu, H.; Win, X.; Xu, X.; Jiao, H.; Schleyer,P.V.R (2005). "Structures and Energies of Isolobal (BCO)n and (CH)n Cages". J. Am. Chem. Soc. 127: 2334–38. doi:10.1021/ja046740f.
- ^ Goldman, A.D.; Tyler, D.R. (1986). "Isolobal Photochemical Reduction of CpW(CO)3CH3 (Cp = η5-C5H5) to CpW(CO)3-; An Isolobal Analogy to the Disproportionation of Cp2Mo2(CO)6". J. Am. Chem. Soc. 108: 89–94. doi:10.1021/ja00261a015.