Fuzzy logic is a modern reasoning method in order to imitates the human ability to make rational decisions with only imperfect information.
This method was designed to overcome the inherent limitations of logical systems based on on classical axioms. These axioms, or principles, dictate that sound arguments that can be evaluated affirmed or denied clearly true or false
mathematically rigorous method of reasoning
of two-value logical systems, whether traditional or modern, based on classical axioms. These axioms dictate that a sound argument is one that can always be affirmed or denied without contradiction. For instance, Boolean algebra—which is the basis for digital computers—require variables that accept either the integer 0 for false or 1 for true. A truth value between 0 and 1 is invalid, as is assigning both 0 and 1.
, whether traditional or modern, founded on the classical axioms, which define sound arguments as ones that can be clearly affirmed or denied without contradiction. True and false are the only options.
A sound argument, according to these earlier methods, can be clearly affirmed or denied without contradiction.
These earlier systems, by definition, only allow two values—true or false—.
, reasons and conclusions can only be evalu
Computer logic gates, for instance,
By accepting a range of truth values, this mathematically rigorous method breaks with the foundational principles of classical logic and its modern descendants. In digital computer logic, for instance, only the integers 0 or 1 are accepted as truth values, respectively representing true and false.
that are based on principles only allow two truth values: .
defining principles, which . .
Fuzzy logic, on the other hand, the truth value of variables may be any real number between 0 and 1. It is employed to handle the concept of partial truth, where the truth value may range between completely true and completely false.[1] By contrast,
The term fuzzy logic was introduced with the 1965 proposal of fuzzy set theory by scientist Lotfi Zadeh.[2][3] Fuzzy logic had, however, been studied since the 1920s, as infinite-valued logic—notably by Łukasiewicz and Tarski.[4]
Fuzzy logic is based on the observation that people make decisions based on imprecise and non-numerical information. Fuzzy models or sets are mathematical means of representing vagueness and imprecise information (hence the term fuzzy). These models have the capability of recognising, representing, manipulating, interpreting, and using data and information that are vague and lack certainty.[5][6]
Fuzzy logic has been applied to many fields, from control theory to artificial intelligence.
Overview
editClassical logic only permits conclusions that are either true or false. However, there are also propositions with variable answers, such as one might find when asking a group of people to identify a color. In such instances, the truth appears as the result of reasoning from inexact or partial knowledge in which the sampled answers are mapped on a spectrum.[7]
Both degrees of truth and probabilities range between 0 and 1 and hence may seem similar at first, but fuzzy logic uses degrees of truth as a mathematical model of vagueness, while probability is a mathematical model of ignorance.[8]
Applying truth values
editA basic application might characterize various sub-ranges of a continuous variable. For instance, a temperature measurement for anti-lock brakes might have several separate membership functions defining particular temperature ranges needed to control the brakes properly. Each function maps the same temperature value to a truth value in the 0 to 1 range. These truth values can then be used to determine how the brakes should be controlled.[9] Fuzzy set theory provides a means for representing uncertainty.
Linguistic variables
editIn fuzzy logic applications, non-numeric values are often used to facilitate the expression of rules and facts.[10]
A linguistic variable such as age may accept values such as young and its antonym old. Because natural languages do not always contain enough value terms to express a fuzzy value scale, it is common practice to modify linguistic values with adjectives or adverbs. For example, we can use the hedges rather and somewhat to construct the additional values rather old or somewhat young. [11]
Rule-Based Systems
editIn mathematical logic, there are several formal systems of "fuzzy logic", most of which are in the family of t-norm fuzzy logics.
Propositional fuzzy logics
editThe most important propositional fuzzy logics are:
- Monoidal t-norm-based propositional fuzzy logic MTL is an axiomatization of logic where conjunction is defined by a left continuous t-norm and implication is defined as the residuum of the t-norm. Its models correspond to MTL-algebras that are pre-linear commutative bounded integral residuated lattices.
- Basic propositional fuzzy logic BL is an extension of MTL logic where conjunction is defined by a continuous t-norm, and implication is also defined as the residuum of the t-norm. Its models correspond to BL-algebras.
- Łukasiewicz fuzzy logic is the extension of basic fuzzy logic BL where standard conjunction is the Łukasiewicz t-norm. It has the axioms of basic fuzzy logic plus an axiom of double negation, and its models correspond to MV-algebras.
- Gödel fuzzy logic is the extension of basic fuzzy logic BL where conjunction is the Gödel t-norm (that is, minimum). It has the axioms of BL plus an axiom of idempotence of conjunction, and its models are called G-algebras.
- Product fuzzy logic is the extension of basic fuzzy logic BL where conjunction is the product t-norm. It has the axioms of BL plus another axiom for cancellativity of conjunction, and its models are called product algebras.
- Fuzzy logic with evaluated syntax (sometimes also called Pavelka's logic), denoted by EVŁ, is a further generalization of mathematical fuzzy logic. While the above kinds of fuzzy logic have traditional syntax and many-valued semantics, in EVŁ syntax is also evaluated. This means that each formula has an evaluation. Axiomatization of EVŁ stems from Łukasziewicz fuzzy logic. A generalization of the classical Gödel completeness theorem is provable in EVŁ[citation needed].
Mamdani
editThe most well-known system is the Mamdani rule-based one. It uses the following rules:
- Fuzzify all input values into fuzzy membership functions.
- Execute all applicable rules in the rulebase to compute the fuzzy output functions.
- De-fuzzify the fuzzy output functions to get "crisp" output values.
Fuzzification
editFuzzification is the process of assigning the numerical input of a system to fuzzy sets with some degree of membership. This degree of membership may be anywhere within the interval [0,1]. If it is 0 then the value does not belong to the given fuzzy set, and if it is 1 then the value completely belongs within the fuzzy set. Any value between 0 and 1 represents the degree of uncertainty that the value belongs in the set. These fuzzy sets are typically described by words, and so by assigning the system input to fuzzy sets, we can reason with it in a linguistically natural manner.
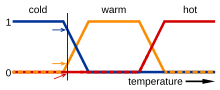
For example, in the image below the meanings of the expressions cold, warm, and hot are represented by functions mapping a temperature scale. A point on that scale has three "truth values"—one for each of the three functions. The vertical line in the image represents a particular temperature that the three arrows (truth values) gauge. Since the red arrow points to zero, this temperature may be interpreted as "not hot"; i.e. this temperature has zero membership in the fuzzy set "hot". The orange arrow (pointing at 0.2) may describe it as "slightly warm" and the blue arrow (pointing at 0.8) "fairly cold". Therefore, this temperature has 0.2 membership in the fuzzy set "warm" and 0.8 membership in the fuzzy set "cold". The degree of membership assigned for each fuzzy set is the result of fuzzification.
Fuzzy sets are often defined as triangle or trapezoid-shaped curves, as each value will have a slope where the value is increasing, a peak where the value is equal to 1 (which can have a length of 0 or greater) and a slope where the value is decreasing.[citation needed] They can also be defined using a sigmoid function.[12] One common case is the standard logistic function defined as
which has the following symmetry property
From this it follows that
Fuzzy logic operators
editFuzzy logic works with membership values in a way that mimics Boolean logic. To this end, replacements for basic operators AND, OR, NOT must be available. There are several ways to this. A common replacement is called the Zadeh operators:
| Boolean | Fuzzy |
|---|---|
| AND(x,y) | MIN(x,y) |
| OR(x,y) | MAX(x,y) |
| NOT(x) | 1 – x |
For TRUE/1 and FALSE/0, the fuzzy expressions produce the same result as the Boolean expressions.
There are also other operators, more linguistic in nature, called hedges that can be applied. These are generally adverbs such as very, or somewhat, which modify the meaning of a set using a mathematical formula.[citation needed]
However, an arbitrary choice table does not always define a fuzzy logic function. In the paper,[13] a criterion has been formulated to recognize whether a given choice table defines a fuzzy logic function and a simple algorithm of fuzzy logic function synthesis has been proposed based on introduced concepts of constituents of minimum and maximum. A fuzzy logic function represents a disjunction of constituents of minimum, where a constituent of minimum is a conjunction of variables of the current area greater than or equal to the function value in this area (to the right of the function value in the inequality, including the function value).
Another set of AND/OR operators is based on multiplication, where
x AND y = x*y
NOT x = 1 - x
Hence,
x OR y = NOT( AND( NOT(x), NOT(y) ) )
x OR y = NOT( AND(1-x, 1-y) )
x OR y = NOT( (1-x)*(1-y) )
x OR y = 1-(1-x)*(1-y)
x OR y = x+y-xy
Given any two of AND/OR/NOT, it is possible to derive the third. The generalization of AND is known as a t-norm.
IF-THEN rules
editIF-THEN rules map input or computed truth values to desired output truth values. Example:
IF temperature IS very cold THEN fan_speed is stopped
IF temperature IS cold THEN fan_speed is slow
IF temperature IS warm THEN fan_speed is moderate
IF temperature IS hot THEN fan_speed is high
Given a certain temperature, the fuzzy variable hot has a certain truth value, which is copied to the high variable.
Should an output variable occur in several THEN parts, then the values from the respective IF parts are combined using the OR operator.
Defuzzification
editThe goal is to get a continuous variable from fuzzy truth values.[citation needed]
This would be easy if the output truth values were exactly those obtained from fuzzification of a given number. Since, however, all output truth values are computed independently, in most cases they do not represent such a set of numbers.[citation needed] One has then to decide for a number that matches best the "intention" encoded in the truth value. For example, for several truth values of fan_speed, an actual speed must be found that best fits the computed truth values of the variables 'slow', 'moderate' and so on. [citation needed]
There is no single algorithm for this purpose.
A common algorithm is
- For each truth value, cut the membership function at this value
- Combine the resulting curves using the OR operator
- Find the center-of-weight of the area under the curve
- The x position of this center is then the final output.
Takagi-Sugeno-Kang (TSK)
editThe TSK system is similar to Mamdani, but the defuzzification process is included in the execution of the fuzzy rules. These are also adapted, so that instead the consequent of the rule is represented through a polynomial function (usually constant or linear). An example of a rule with a constant output would be:
IF temperature IS very cold = 2
In this case, the output will be equal to the constant of the consequent (e.g. 2). In most scenarios we would have an entire rule base, with 2 or more rules. If this is the case, the output of the entire rule base will be the average of the consequent of each rule i (Yi), weighted according to the membership value of its antededent (hi):
An example of a rule with a linear output would be instead:
IF temperature IS very cold AND humidity IS high = 2 * temperature + 1 * humidity
In this case, the output of the rule will be the result of function in the consequent. The variables within the function represent the membership values after fuzzification, not the crisp values. Same as before, in case we have an entire rule base with 2 or more rules, the total output will be the weighted average between the output of each rule.
The main advantage of using TSK over Mamdani is that is computational efficient and works well within other algorithms, such as PID control and with optimization algorithms. It can also guarantee the continuity of the output surface. However, Mamdani is more intuitive and easier to work with by people. Hence, TSK is usually used within other complex methods, such as in Adaptive neuro fuzzy inference systems.
Forming a consensus of inputs and fuzzy rules
editSince the fuzzy system output is a consensus of all of the inputs and all of the rules, fuzzy logic systems can be well behaved when input values are not available or are not trustworthy. Weightings can be optionally added to each rule in the rulebase and weightings can be used to regulate the degree to which a rule affects the output values. These rule weightings can be based upon the priority, reliability or consistency of each rule. These rule weightings may be static or can be changed dynamically, even based upon the output from other rules.
Applications
editUnlike Boolean algebra, fuzzy logic can easily deal with imprecise information and uncertainty, making it highly suitable for solving real-world problems. In fact, starting with a 1980s boom in Japan, fuzzy-logic applications have become commonplace. By the end of the twentieth century, many consumer products with automatic controls, from cameras and to air conditioning and washer machines, incorporated fuzzy rules alongside more conventional methods.
Rule-Based Control Systems
editReal-world systems, because they are dynamic and nonlinear, are difficult to control using traditional Boolean logic.
Almost all non-theoretical systems are dynamic and nonlinear. — which have input values that change over time — that is to say, dynamic —but those changes are often unproportionally dynamic — meaning its input values change over time — and nonlinear —— typically Controlling nonlinear dynamical systems before Since the 1990s, rule-based fuzzy logic has been a dominant design methodology for controlling nonlinear dynamical systems. These systems, which vary over time,
Unlike simple linear systems. these systems seem counterintuitive, even unpredictable, these systems receive variable input which are such as heating .
Fuzzy logic allows control systems to include vague rules, like "if you are close to the destination station and moving fast, increase the train's brake pressure." Once inside the system, these imprecise rules can then be numerically refined.
Japanese and Chinese researchers
Many of the early successful applications of fuzzy logic were implemented in Japan. The first notable application was on the subway train in Sendai, in which fuzzy logic was able to improve the economy, comfort, and precision of the ride[citation needed]. It has also been used for handwriting recognition in Sony pocket computers, helicopter flight aids, subway system controls, improving automobile fuel efficiency, single-button washing machine controls, automatic power controls in vacuum cleaners, and early recognition of earthquakes through the Institute of Seismology Bureau of Meteorology, Japan.[14] "It turns out," as Charles Elkan writes, "the useful applications of fuzzy logic are not in high-level artificial intelligence but rather in lower-level machine control, especially in consumer products."[15]
Artificial intelligence
editModern AI typically relies on fuzzy logic. A neural network will take a variety of valued inputs, give them different weights in relation to each other, and arrive at a decision which normally also has a value. Nowhere in that process is there anything like the sequences of either-or decisions which characterize non-fuzzy mathematics, almost all of computer programming, and digital electronics. In the 1980s, researchers were divided about the most effective approach to machine learning: "common sense" models or neural networks. The former approach requires large decision trees and uses binary logic, matching the hardware on which it runs. The physical devices might be limited to binary logic, but AI can use software for its calculations. Neural networks take this approach, which results in more accurate models of complex situations. Neural networks soon found their way onto a multitude of electronic device. [16]
Medical decision making
editFuzzy logic is an important concept in medical decision making. Since medical and healthcare data can be subjective or fuzzy, applications in this domain have a great potential to benefit a lot by using fuzzy logic based approaches.
Fuzzy logic can be used in many different aspects within the medical decision making framework. Such aspects include[17][18][19][clarification needed] in medical image analysis, biomedical signal analysis, segmentation of images[20] or signals, and feature extraction / selection of images[20] or signals.[21]
The biggest question in this application area is how much useful information can be derived when using fuzzy logic. A major challenge is how to derive the required fuzzy data. This is even more challenging when one has to elicit such data from humans (usually, patients). As has been said
"The envelope of what can be achieved and what cannot be achieved in medical diagnosis, ironically, is itself a fuzzy one"
— Seven Challenges, 2019.[22]
How to elicit fuzzy data, and how to validate the accuracy of the data is still an ongoing effort strongly related to the application of fuzzy logic. The problem of assessing the quality of fuzzy data is a difficult one. This is why fuzzy logic is a highly promising possibility within the medical decision making application area but still requires more research to achieve its full potential.[22] Although the concept of using fuzzy logic in medical decision making is exciting, there are still several challenges that fuzzy approaches face within the medical decision making framework.
Image-based computer-aided diagnosis
editOne of the common application areas that use fuzzy logic is image-based computer-aided diagnosis (CAD) in medicine.[23] CAD is a computerized set of inter-related tools that can be used to aid physicians in their diagnostic decision-making. For example, when a physician finds a lesion that is abnormal but still at a very early stage of development he/she may use a CAD approach to characterize the lesion and diagnose its nature. Fuzzy logic can be highly appropriate to describe key characteristics of this lesion.
Fuzzy Databases
editOnce fuzzy relations are defined, it is possible to develop fuzzy relational databases. The first fuzzy relational database, FRDB, appeared in Maria Zemankova's dissertation (1983). Later, some other models arose like the Buckles-Petry model, the Prade-Testemale Model, the Umano-Fukami model or the GEFRED model by J.M. Medina, M.A. Vila et al.
Fuzzy querying languages have been defined, such as the SQLf by P. Bosc et al. and the FSQL by J. Galindo et al. These languages define some structures in order to include fuzzy aspects in the SQL statements, like fuzzy conditions, fuzzy comparators, fuzzy constants, fuzzy constraints, fuzzy thresholds, linguistic labels etc.
Logical analysis
editIn mathematical logic, there are several formal systems of "fuzzy logic", most of which are in the family of t-norm fuzzy logics.
Propositional fuzzy logics
editThe most important propositional fuzzy logics are:
- Monoidal t-norm-based propositional fuzzy logic MTL is an axiomatization of logic where conjunction is defined by a left continuous t-norm and implication is defined as the residuum of the t-norm. Its models correspond to MTL-algebras that are pre-linear commutative bounded integral residuated lattices.
- Basic propositional fuzzy logic BL is an extension of MTL logic where conjunction is defined by a continuous t-norm, and implication is also defined as the residuum of the t-norm. Its models correspond to BL-algebras.
- Łukasiewicz fuzzy logic is the extension of basic fuzzy logic BL where standard conjunction is the Łukasiewicz t-norm. It has the axioms of basic fuzzy logic plus an axiom of double negation, and its models correspond to MV-algebras.
- Gödel fuzzy logic is the extension of basic fuzzy logic BL where conjunction is the Gödel t-norm (that is, minimum). It has the axioms of BL plus an axiom of idempotence of conjunction, and its models are called G-algebras.
- Product fuzzy logic is the extension of basic fuzzy logic BL where conjunction is the product t-norm. It has the axioms of BL plus another axiom for cancellativity of conjunction, and its models are called product algebras.
- Fuzzy logic with evaluated syntax (sometimes also called Pavelka's logic), denoted by EVŁ, is a further generalization of mathematical fuzzy logic. While the above kinds of fuzzy logic have traditional syntax and many-valued semantics, in EVŁ syntax is also evaluated. This means that each formula has an evaluation. Axiomatization of EVŁ stems from Łukasziewicz fuzzy logic. A generalization of the classical Gödel completeness theorem is provable in EVŁ[citation needed].
Decidability Issues
editThe notions of a "decidable subset" and "recursively enumerable subset" are basic ones for classical mathematics and classical logic. Thus the question of a suitable extension of them to fuzzy set theory is a crucial one. A first proposal in such a direction was made by E.S. Santos by the notions of fuzzy Turing machine, Markov normal fuzzy algorithm and fuzzy program (see Santos 1970). Successively, L. Biacino and G. Gerla argued that the proposed definitions are rather questionable. For example, in [24] one shows that the fuzzy Turing machines are not adequate for fuzzy language theory since there are natural fuzzy languages intuitively computable that cannot be recognized by a fuzzy Turing Machine. Then they proposed the following definitions. Denote by Ü the set of rational numbers in [0,1]. Then a fuzzy subset s : S [0,1] of a set S is recursively enumerable if a recursive map h : S×N Ü exists such that, for every x in S, the function h(x,n) is increasing with respect to n and s(x) = lim h(x,n). We say that s is decidable if both s and its complement –s are recursively enumerable. An extension of such a theory to the general case of the L-subsets is possible (see Gerla 2006). The proposed definitions are well related with fuzzy logic. Indeed, the following theorem holds true (provided that the deduction apparatus of the considered fuzzy logic satisfies some obvious effectiveness property).
Any "axiomatizable" fuzzy theory is recursively enumerable. In particular, the fuzzy set of logically true formulas is recursively enumerable in spite of the fact that the crisp set of valid formulas is not recursively enumerable, in general. Moreover, any axiomatizable and complete theory is decidable.
It is an open question to give support for a "Church thesis" for fuzzy mathematics, the proposed notion of recursive enumerability for fuzzy subsets is the adequate one. In order to solve this, an extension of the notions of fuzzy grammar and fuzzy Turing machine are necessary. Another open question is to start from this notion to find an extension of Gödel's theorems to fuzzy logic.
Compared to Other Logics
editProbability
editFuzzy logic and probability address different forms of uncertainty. While both fuzzy logic and probability theory can represent degrees of certain kinds of subjective belief, fuzzy set theory uses the concept of fuzzy set membership, i.e., how much an observation is within a vaguely defined set, and probability theory uses the concept of subjective probability, i.e., frequency of occurrence or likelihood of some event or condition [clarification needed]. The concept of fuzzy sets was developed in the mid-twentieth century at Berkeley [25] as a response to the lack of a probability theory for jointly modelling uncertainty and vagueness.[26]
Bart Kosko claims in Fuzziness vs. Probability[27] that probability theory is a subtheory of fuzzy logic, as questions of degrees of belief in mutually-exclusive set membership in probability theory can be represented as certain cases of non-mutually-exclusive graded membership in fuzzy theory. In that context, he also derives Bayes' theorem from the concept of fuzzy subsethood. Lotfi A. Zadeh argues that fuzzy logic is different in character from probability, and is not a replacement for it. He fuzzified probability to fuzzy probability and also generalized it to possibility theory.[28]
More generally, fuzzy logic is one of many different extensions to classical logic intended to deal with issues of uncertainty outside of the scope of classical logic, the inapplicability of probability theory in many domains, and the paradoxes of Dempster–Shafer theory.
Ecorithms
editComputational theorist Leslie Valiant uses the term ecorithms to describe how many less exact systems and techniques like fuzzy logic (and "less robust" logic) can be applied to learning algorithms. Valiant essentially redefines machine learning as evolutionary. In general use, ecorithms are algorithms that learn from their more complex environments (hence eco-) to generalize, approximate and simplify solution logic. Like fuzzy logic, they are methods used to overcome continuous variables or systems too complex to completely enumerate or understand discretely or exactly.[29] Ecorithms and fuzzy logic also have the common property of dealing with possibilities more than probabilities, although feedback and feed forward, basically stochastic weights, are a feature of both when dealing with, for example, dynamical systems.
Branches of fuzzy logic
editPredicate fuzzy logics
editSimilar to the way predicate logic is created from propositional logic, predicate fuzzy logics extend fuzzy systems by universal and existential quantifiers. The semantics of the universal quantifier in t-norm fuzzy logics is the infimum of the truth degrees of the instances of the quantified subformula while the semantics of the existential quantifier is the supremum of the same.
Compensatory fuzzy logic
editCompensatory fuzzy logic (CFL) has modified rules for conjunction and disjunction. When the truth value of one component of a conjunction or disjunction is increased or decreased, the other component is decreased or increased to compensate. This increase or decrease in truth value may be offset by the increase or decrease in another component. An offset may be blocked when certain thresholds are met. Proponents[who?] claim that CFL allows for better computational semantic behaviors and mimic natural language.[vague][30][31]
Compensatory fuzzy logic consists of four continuous operators: conjunction (c), disjunction (d), fuzzy strict order (or), and negation (n). The conjunction is the geometric mean and its dual as conjunctive and disjunctive operators.[32]
Markup Language Standardization
editThe IEEE 1855, the IEEE STANDARD 1855–2016, is about a specification language named Fuzzy Markup Language (FML)[33] developed by the IEEE Standards Association. FML allows modelling a fuzzy logic system in a human-readable and hardware independent way. FML is based on eXtensible Markup Language (XML). The designers of fuzzy systems with FML have a unified and high-level methodology for describing interoperable fuzzy systems. IEEE STANDARD 1855–2016 uses the W3C XML Schema definition language to define the syntax and semantics of the FML programs.
Prior to the introduction of FML, fuzzy logic practitioners could exchange information about their fuzzy algorithms by adding to their software functions the ability to read, correctly parse, and store the result of their work in a form compatible with the Fuzzy Control Language (FCL) described and specified by Part 7 of IEC 61131.[34][35]
See also
edit- Adaptive neuro fuzzy inference system (ANFIS)
- Artificial neural network
- Defuzzification
- Expert system
- False dilemma
- Fuzzy architectural spatial analysis
- Fuzzy classification
- Fuzzy concept
- Fuzzy Control Language
- Fuzzy control system
- Fuzzy electronics
- Fuzzy subalgebra
- FuzzyCLIPS
- High Performance Fuzzy Computing
- IEEE Transactions on Fuzzy Systems
- Interval finite element
- Machine learning
- Neuro-fuzzy
- Noise-based logic
- Rough set
- Sorites paradox
- Type-2 fuzzy sets and systems
- Vector logic
References
edit- ^ Novák, V.; Perfilieva, I.; Močkoř, J. (1999). Mathematical principles of fuzzy logic. Dordrecht: Kluwer Academic. ISBN 978-0-7923-8595-0.
- ^ "Fuzzy Logic". Stanford Encyclopedia of Philosophy. Bryant University. 2006-07-23. Retrieved 2008-09-30.
- ^ Zadeh, L.A. (June 1965). "Fuzzy sets". Information and Control. 8 (3). San Diego: 338–353. doi:10.1016/S0019-9958(65)90241-X. ISSN 0019-9958. Zbl 0139.24606. Wikidata Q25938993.
- ^ Pelletier, Francis Jeffry (2000). "Review of Metamathematics of fuzzy logics" (PDF). The Bulletin of Symbolic Logic. 6 (3): 342–346. doi:10.2307/421060. JSTOR 421060. Archived (PDF) from the original on 2016-03-03.
- ^ "What is Fuzzy Logic? "Mechanical Engineering Discussion Forum"".
- ^ Robert Babuška (6 December 2012). Fuzzy Modeling for Control. Springer Science & Business Media. ISBN 978-94-011-4868-9.
- ^ "Fuzzy Logic". Archived from the original on 2021-12-05.}|title= Fuzzy Logic
- ^ Asli, Kaveh Hariri; Aliyev, Soltan Ali Ogli; Thomas, Sabu; Gopakumar, Deepu A. (2017-11-23). Handbook of Research for Fluid and Solid Mechanics: Theory, Simulation, and Experiment. CRC Press. ISBN 9781315341507.
- ^ Chaudhuri, Arindam; Mandaviya, Krupa; Badelia, Pratixa; Ghosh, Soumya K. (2016-12-23). Optical Character Recognition Systems for Different Languages with Soft Computing. Springer. ISBN 9783319502526.
- ^ Zadeh, L. A.; et al. (1996). Fuzzy Sets, Fuzzy Logic, Fuzzy Systems. World Scientific Press. ISBN 978-981-02-2421-9.
- ^ L. A. Zadeh "The concept of a linguistic variable and its application to approximate reasoning" Information Sciences Volume 8, Issue 3, 1975, Pages 199-249
- ^ Wierman, Mark J. "An Introduction to the Mathematics of Uncertainty: including Set Theory, Logic, Probability, Fuzzy Sets, Rough Sets, and Evidence Theory" (PDF). Creighton University. Archived (PDF) from the original on 30 July 2012. Retrieved 16 July 2016.
- ^ Zaitsev, D.A.; Sarbei, V.G.; Sleptsov, A.I. (1998). "Synthesis of continuous-valued logic functions defined in tabular form". Cybernetics and Systems Analysis. 34 (2): 190–195. doi:10.1007/BF02742068. S2CID 120220846.
- ^ Bansod, Nitin A; Kulkarni, Marshall; Patil, S.H. (2005). "Soft Computing- A Fuzzy Logic Approach". In Bharati Vidyapeeth College of Engineering (ed.). Soft Computing. Allied Publishers. p. 73. ISBN 978-81-7764-632-0. Retrieved 9 November 2018.
- ^ "What is 'fuzzy logic'? Are there computers that are inherently fuzzy and do not apply the usual binary logic?". Scientific American. Retrieved 5 May 2018.
- ^ Elkan, Charles (1994). "The paradoxical success of fuzzy logic". IEEE Expert. 9 (4): 3–49. CiteSeerX 10.1.1.100.8402. doi:10.1109/64.336150. S2CID 113687.
- ^ Lin KP, Chang HF, Chen TL, Lu YM, and Wang CH (2016). "Intuitionistic fuzzy C-regression by using least squares support vector regression". Expert Systems with Applications. 64: 296–304. doi:10.1016/j.eswa.2016.07.040.
- ^ Deng H, Deng W, Sun X, Ye C, and Zhou X (2016). "Adaptive intuitionistic fuzzy enhancement of brain tumor MR images". Scientific Reports. 6: 35760. Bibcode:2016NatSR...635760D. doi:10.1038/srep35760. PMC 5082372. PMID 27786240.
- ^ Vlachos IK, Sergiadis GD (2007). "Intuitionistic fuzzy information–applications to pattern recognition". Pattern Recognition Letters. 28 (2): 197–206. Bibcode:2007PaReL..28..197V. doi:10.1016/j.patrec.2006.07.004.
- ^ a b Gonzalez-Hidalgo, Manuel; Munar, Marc; Bibiloni, Pedro; Moya-Alcover, Gabriel; Craus-Miguel, Andrea; Segura-Sampedro, Juan Jose (October 2019). "Detection of infected wounds in abdominal surgery images using fuzzy logic and fuzzy sets". 2019 International Conference on Wireless and Mobile Computing, Networking and Communications (WiMob). Barcelona, Spain: IEEE: 99–106. doi:10.1109/WiMOB.2019.8923289. ISBN 978-1-7281-3316-4. S2CID 208880793.
- ^ Das S, Guha D, and Dutta B (2016). "Medical diagnosis with the aid of using fuzzy logic and intuitionistic fuzzy logic". Applied Intelligence. 45 (3): 850–867. doi:10.1007/s10489-016-0792-0. S2CID 14590409.
- ^ a b Yanase, Juri; Triantaphyllou, Evangelos (2019). "The Seven Key Challenges for the Future of Computer-Aided Diagnosis in Medicine". International Journal of Medical Informatics. 129: 413–422. doi:10.1016/j.ijmedinf.2019.06.017. PMID 31445285.
- ^ Yanase, Juri; Triantaphyllou, Evangelos (2019). "A Systematic Survey of Computer-Aided Diagnosis in Medicine: Past and Present Developments". Expert Systems with Applications. 138: 112821. doi:10.1016/j.eswa.2019.112821.
- ^ Gerla, G. (2016). "Comments on some theories of fuzzy computation". International Journal of General Systems. 45 (4): 372–392. Bibcode:2016IJGS...45..372G. doi:10.1080/03081079.2015.1076403. S2CID 22577357.
- ^ "Lofti Zadeh Berkeley". Archived from the original on 2017-02-11.
- ^ Mares, Milan (2006). "Fuzzy Sets". Scholarpedia. 1 (10): 2031. Bibcode:2006SchpJ...1.2031M. doi:10.4249/scholarpedia.2031.
- ^ Kosko, Bart. "Fuzziness vs. Probability" (PDF). University of South California. Retrieved 9 November 2018.
- ^ Novák, V (2005). "Are fuzzy sets a reasonable tool for modeling vague phenomena?". Fuzzy Sets and Systems. 156 (3): 341–348. doi:10.1016/j.fss.2005.05.029.
- ^ Valiant, Leslie (2013). Probably Approximately Correct: Nature's Algorithms for Learning and Prospering in a Complex World. New York: Basic Books. ISBN 978-0465032716.
- ^ "Archived copy" (PDF). Archived (PDF) from the original on 2015-10-04. Retrieved 2015-10-02.
{{cite web}}: CS1 maint: archived copy as title (link) - ^ Veri, Francesco (2017). "Fuzzy Multiple Attribute Conditions in fsQCA: Problems and Solutions". Sociological Methods & Research. 49 (2): 312–355. doi:10.1177/0049124117729693. S2CID 125146607.
- ^ Cejas, Jesús (2011). "Compensatory Fuzzy Logic". Revista de Ingeniería Industrial. ISSN 1815-5936.
- ^ Acampora, Giovanni; Di Stefano, Bruno N.; Vitiello, Autilia (2016). "IEEE 1855™: The First IEEE Standard Sponsored by IEEE Computational Intelligence Society [Society Briefs]". IEEE Computational Intelligence Magazine. 11 (4): 4–6. doi:10.1109/MCI.2016.2602068.
- ^ Di Stefano, Bruno N. (2013). "On the Need of a Standard Language for Designing Fuzzy Systems". On the Power of Fuzzy Markup Language. Studies in Fuzziness and Soft Computing. Vol. 296. pp. 3–15. doi:10.1007/978-3-642-35488-5_1. ISBN 978-3-642-35487-8. ISSN 1434-9922.
- ^ Acampora, Giovanni; Loia, Vincenzo; Lee, Chang-Shing; Wang, Mei-Hui (2013). On the Power of Fuzzy Markup Language. Studies in Fuzziness and Soft Computing. Vol. 296. doi:10.1007/978-3-642-35488-5. ISBN 978-3-642-35487-8. ISSN 1434-9922.
{{cite book}}:|journal=ignored (help)
Bibliography
edit- Arabacioglu, B. C. (2010). "Using fuzzy inference system for architectural space analysis". Applied Soft Computing. 10 (3): 926–937. doi:10.1016/j.asoc.2009.10.011.
- Biacino, L.; Gerla, G. (2002). "Fuzzy logic, continuity and effectiveness". Archive for Mathematical Logic. 41 (7): 643–667. CiteSeerX 10.1.1.2.8029. doi:10.1007/s001530100128. ISSN 0933-5846. S2CID 12513452.
- Cox, Earl (1994). The fuzzy systems handbook: a practitioner's guide to building, using, maintaining fuzzy systems. Boston: AP Professional. ISBN 978-0-12-194270-0.
- Gerla, Giangiacomo (2006). "Effectiveness and Multivalued Logics". Journal of Symbolic Logic. 71 (1): 137–162. doi:10.2178/jsl/1140641166. ISSN 0022-4812. S2CID 12322009.
- Hájek, Petr (1998). Metamathematics of fuzzy logic. Dordrecht: Kluwer. ISBN 978-0-7923-5238-9.
- Hájek, Petr (1995). "Fuzzy logic and arithmetical hierarchy". Fuzzy Sets and Systems. 3 (8): 359–363. doi:10.1016/0165-0114(94)00299-M. ISSN 0165-0114.
- Halpern, Joseph Y. (2003). Reasoning about uncertainty. Cambridge, Massachusetts: MIT Press. ISBN 978-0-262-08320-1.
- Höppner, Frank; Klawonn, F.; Kruse, R.; Runkler, T. (1999). Fuzzy cluster analysis: methods for classification, data analysis and image recognition. New York: John Wiley. ISBN 978-0-471-98864-9.
- Ibrahim, Ahmad M. (1997). Introduction to Applied Fuzzy Electronics. Englewood Cliffs, NJ: Prentice Hall. ISBN 978-0-13-206400-2.
- Klir, George Jiří; Folger, Tina A. (1988). Fuzzy sets, uncertainty, and information. Englewood Cliffs, NJ: Prentice Hall. ISBN 978-0-13-345984-5.
- Klir, George Jiří; St. Clair, Ute H.; Yuan, Bo (1997). Fuzzy set theory: foundations and applications. Englewood Cliffs, NJ: Prentice Hall. ISBN 978-0-13-341058-7.
- Klir, George Jiří; Yuan, Bo (1995). Fuzzy sets and fuzzy logic: theory and applications. Upper Saddle River, NJ: Prentice Hall PTR. ISBN 978-0-13-101171-7.
- Kosko, Bart (1993). Fuzzy thinking: the new science of fuzzy logic. New York: Hyperion. ISBN 978-0-7868-8021-8.
- Kosko, Bart; Isaka, Satoru (July 1993). "Fuzzy Logic". Scientific American. 269 (1): 76–81. Bibcode:1993SciAm.269a..76K. doi:10.1038/scientificamerican0793-76.
- Lohani, A. K.; Goel, N. K.; Bhatia, K. K. S. (2006). "Takagi–Sugeno fuzzy inference system for modeling stage–discharge relationship". Journal of Hydrology. 331 (1): 146–160. Bibcode:2006JHyd..331..146L. doi:10.1016/j.jhydrol.2006.05.007.
- Lohani, A. K.; Goel, N. K.; Bhatia, K. K. S. (2007). "Deriving stage–discharge–sediment concentration relationships using fuzzy logic". Hydrological Sciences Journal. 52 (4): 793–807. doi:10.1623/hysj.52.4.793. S2CID 117782707.
- Lohani, A. K.; Goel, N. K.; Bhatia, K. K. S. (2012). "Hydrological time series modeling: A comparison between adaptive neuro-fuzzy, neural network and autoregressive techniques". Journal of Hydrology. 442–443 (6): 23–35. Bibcode:2012JHyd..442...23L. doi:10.1016/j.jhydrol.2012.03.031.
- Masmoudi, Malek; Haït, Alain (November 2012). "Fuzzy uncertainty modelling for project planning; application to helicopter maintenance" (PDF). International Journal of Production Research. 50 (24).
- Merigo, Jose M.; Gil-Lafuente, Anna M.; Yager, Ronald R. (2015). "An overview of fuzzy research with bibliometric indicators". Applied Soft Computing. 27: 420–433. doi:10.1016/j.asoc.2014.10.035. ISSN 1568-4946.
- Mironov, A. (2005). "Fuzzy modal logic". Journal of Mathematical Sciences. 128 (6): 3461–3483. doi:10.1007/s10958-005-0281-1. ISSN 1072-3374. S2CID 120674564.
- Montagna, F. (2001). "Three complexity problems in quantified fuzzy logic". Studia Logica. 68 (1): 143–152. doi:10.1023/A:1011958407631. ISSN 0039-3215. S2CID 20035297.
- Mundici, Daniele; Cignoli, Roberto; D'Ottaviano, Itala M. L. (1999). Algebraic foundations of many-valued reasoning. Dordrecht: Kluwer Academic. ISBN 978-0-7923-6009-4.
- Novák, Vilém (1989). Fuzzy Sets and Their Applications. Bristol: Adam Hilger. ISBN 978-0-85274-583-0.
- Novák, Vilém (2005). "On fuzzy type theory". Fuzzy Sets and Systems. 149 (2): 235–273. doi:10.1016/j.fss.2004.03.027.
- Novák, Vilém; Perfilieva, Irina; Močkoř, Jiří (1999). Mathematical principles of fuzzy logic. Dordrecht: Kluwer Academic. ISBN 978-0-7923-8595-0.
- Onses, Richard (1996). Second Order Experton: A new Tool for Changing Paradigms in Country Risk Calculation. ISBN 978-84-7719-558-0.
- Onses, Richard (1994). Détermination de l´incertitude inhérente aux investissements en Amérique Latine sur la base de la théorie des sous ensembles flous. Barcelona. ISBN 978-84-475-0881-5.
{{cite book}}: CS1 maint: location missing publisher (link) - Passino, Kevin M.; Yurkovich, Stephen (1998). Fuzzy control. Boston: Addison-Wesley. ISBN 978-0-201-18074-9.
- Pedrycz, Witold; Gomide, Fernando (2007). Fuzzy systems engineering: Toward Human-centric Computing. Hoboken: Wiley-Interscience. ISBN 978-0-471-78857-7.
- Pu, Pao Ming; Liu, Ying Ming (1980). "Fuzzy topology. I. Neighborhood structure of a fuzzy point and Moore-Smith convergence". Journal of Mathematical Analysis and Applications. 76 (2): 571–599. doi:10.1016/0022-247X(80)90048-7. ISSN 0022-247X.
- Sahoo, Bhabagrahi; Lohani, A. K.; Sahu, Rohit K. (2006). "Fuzzy multiobjective and linear programming based management models for optimal land-water-crop system planning". Water Resources Management, Springer Netherlands. 20 (6): 931–948. doi:10.1007/s11269-005-9015-x. S2CID 154264034.
- Santos, Eugene S. (1970). "Fuzzy Algorithms". Information and Control. 17 (4): 326–339. doi:10.1016/S0019-9958(70)80032-8.
- Scarpellini, Bruno (1962). "Die Nichaxiomatisierbarkeit des unendlichwertigen Prädikatenkalküls von Łukasiewicz". Journal of Symbolic Logic. 27 (2): 159–170. doi:10.2307/2964111. hdl:20.500.11850/423097. ISSN 0022-4812. JSTOR 2964111.
- Seising, Rudolf (2007). The Fuzzification of Systems. The Genesis of Fuzzy Set Theory and Its Initial Applications -- Developments up to the 1970s. Springer-Verlag. ISBN 978-3-540-71795-9.
- Steeb, Willi-Hans (2008). The Nonlinear Workbook: Chaos, Fractals, Cellular Automata, Neural Networks, Genetic Algorithms, Gene Expression Programming, Support Vector Machine, Wavelets, Hidden Markov Models, Fuzzy Logic with C++, Java and SymbolicC++ Programs (4 ed.). World Scientific. ISBN 978-981-281-852-2.
- Tsitolovsky, Lev; Sandler, Uziel (2008). Neural Cell Behavior and Fuzzy Logic. Springer. ISBN 978-0-387-09542-4.
- Wiedermann, J. (2004). "Characterizing the super-Turing computing power and efficiency of classical fuzzy Turing machines". Theoretical Computer Science. 317 (1–3): 61–69. doi:10.1016/j.tcs.2003.12.004.
- Yager, Ronald R.; Filev, Dimitar P. (1994). Essentials of fuzzy modeling and control. New York: Wiley. ISBN 978-0-471-01761-5.
- Van Pelt, Miles (2008). Fuzzy Logic Applied to Daily Life. Seattle, WA: No No No No Press. ISBN 978-0-252-16341-8.
- Von Altrock, Constantin (1995). Fuzzy logic and NeuroFuzzy applications explained. Upper Saddle River, NJ: Prentice Hall PTR. ISBN 978-0-13-368465-0.
- Wilkinson, R. H. (1963). "A method of generating functions of several variables using analog diode logic". IEEE Transactions on Electronic Computers. 12 (2): 112–129. doi:10.1109/PGEC.1963.263419.
- Zadeh, L. A. (1968). "Fuzzy algorithms". Information and Control. 12 (2): 94–102. doi:10.1016/S0019-9958(68)90211-8. ISSN 0019-9958.
- Zadeh, L.A. (June 1965). "Fuzzy sets". Information and Control. 8 (3). San Diego: 338–353. doi:10.1016/S0019-9958(65)90241-X. ISSN 0019-9958. Zbl 0139.24606. Wikidata Q25938993.
- Zaitsev, D. A.; Sarbei, V. G.; Sleptsov, A. I. (1998). "Synthesis of continuous-valued logic functions defined in tabular form". Cybernetics and Systems Analysis. 34 (2): 190–195. doi:10.1007/BF02742068. S2CID 120220846.
- Zimmermann, H. (2001). Fuzzy set theory and its applications. Boston: Kluwer Academic Publishers. ISBN 978-0-7923-7435-0.
External links
edit- Formal fuzzy logic – article at Citizendium
- IEC 1131-7 CD1 Archived 2021-03-04 at the Wayback Machine IEC 1131-7 CD1 PDF
- Fuzzy Logic – article at Scholarpedia
- Modeling With Words – article at Scholarpedia
- Fuzzy logic – article at Stanford Encyclopedia of Philosophy
- Fuzzy Math – Beginner level introduction to Fuzzy Logic
- Fuzziness and exactness – Fuzziness in everyday life, science, religion, ethics, politics, etc.
- Fuzzylite – A cross-platform, free open-source Fuzzy Logic Control Library written in C++. Also has a very useful graphic user interface in QT4.
- More Flexible Machine Learning – MIT describes one application.
- Semantic Similarity MIT provides details about fuzzy semantic similarity.
Blogosphere
editThe blogosphere is the online milieu, or social environment, structured by the multitude of informal, interconnected webpages that individuals and organizations use to chronicle day-to-day details about their experiences, actions, and thoughts.
Blogs are basically chronological online journals. They are replacing the vanity personal Web pages of the mid to late ‘90s as the way most people attempt to leave their mark on the Internet.[1]
https://chnm.gmu.edu/digitalhistory/links/cached/chapter6/6_13i_weblog.htm#Precursors
In 1999, the popular blogging website Blogger.com was launched, which was later acquired by Google in February 2003.
The same year, WordPress released its first version as a blogging platform in May 2003.
Today, WordPress is the world’s most popular blogging platform powering over 41% of all websites on the internet.
a national phone survey between March 12 and May 20, 2003, 44% of Internet users have created content for the online world through building or posting to Web sites, creating blogs, and sharing files. 2% maintain Web diaries or Web blogs, according to respondents to this phone survey. In other phone surveys prior to this one, and one more recently fielded in early 2004, we have heard that between 2% and 7% of adult Internet users have created diaries or blogs. In this survey we found that 11% of Internet users have read the blogs or diaries of other Internet users. About a third of these blog visitors have posted material to the blog.
Even though only a small number of Internet users are writing blogs, a slightly larger number of Net users are visiting them. Eleven percent of Internet users report visiting blogs written by others. And of these blog readers, a third report posting to or commenting on the blog entries that they have read.
Blog readers most frequently visit the online diaries of friends (56% have done so), strangers (46% have visited the blogs of people they have never met) and family members (a quarter report visiting family blogs).
Power creators might also be called the Bloggers—12% of this group has a blog and close to a third (29%) has ever visited one, compared to less than 3% of other creators, and much lower levels of reported blog visits in the other two groups.
Power creators are also the most likely of all creators to have broadband Internet access—40% of power creators have high-speed access.
The most eager and productive content creators break into three distinct groups:
- Power creators are the Internet users who are most enthusiastic about content-creating activities. They are young – their average age is 25 – and they are more likely than other kinds of creators do things like use instant messaging, play games, and download music. And they are the most likely group to be blogging.
- Older creators have an average age of 58 and are experienced Internet users. They are highly educated, like sharing pictures, and are the most likely of the creator groups to have built their own Web sites. They are also the most likely to have used the Internet for genealogical research.
- Content omnivores are among the heaviest overall users of the Internet. Most are employed. Most log on frequently and spend considerable time online doing a variety of activities. They are likely to have broadband connections at home. The average age of this group is 40
One in five Internet users report visiting online newsgroups, forums where users can post their thoughts to a discussion that takes place over time. More than half of newsgroup users have posted comments to newsgroups, but a mere 4% have used newsgroups as a way to share photo, audio or video files.
This group is also more likely than other content creators to live in rural areas, a factor which may partially explain their somewhat lower level of broadband internet access. Nevertheless the 36% of older creators with broadband is more than the 31% of American Internet-using households with high-speed access. This group is the least likely to live in an urban area.
This group does not engage in a particularly wide variety of online activities. Older creators’ main content creation activity is the building and maintenance of a personal Web site. More than a third (34%) of this group has its own personal Web site. They are also just as likely to use a Web cam (18%) and post photos (36%) and video (8%) to a Web site as power creators. They are just as likely or slightly more likely than other creators to have contributed to or maintain a Web site for a business or an organization.
Similar to other older Americans, Older creators are also more enthusiastic about online genealogical activities than other creators—a third (33%) have ever searched online for information about their family history.
Content omnivores as a group have tried more of all kinds of Internet activities—including content creating ones. They are online frequently, and are more likely than other creators to have emailed, read news or surfed for information on a favorite hobby on a typical day. Still, they differ from power creators in that they have not embraced the newest of the new—most have never used a Web cam (only 13% have), and they do not keep a blog (3% do), though they do visit them, with 17% of Omnivores having ever visited the blog of a friend, relative or stranger.
Omnivores are the workhorses of the content creating crowd—they are online all the time and they also work full-time, with 75% employed full-time and another 7% employed part-time. Surprisingly, another 12% are students. These content creators are, like Older creators, highly educated with high incomes, with half with a college or graduate degree, and half with incomes over $50,000 annually. Omnivores mostly live in suburban (52%) or urban (31%) areas. This group is also contains a slightly larger percentage of women (53% women, 47% men), and is overwhelming made up of parents—69% have children under 18 living at home.
Content omnivores are, by a very slightly margin, the least likely of all content creators to have broadband Internet access. Nevertheless, they are frequent and dedicated users of the Internet and have tried a wide variety of activities. Omnivores seek finance information online (60% have ever done so), visit government Web sites (79% have), buy products and purchase travel online (78% and 73% respectively).
When creating their own content, Omnivores tend toward more tried and true content areas on the Web. More than a quarter (28%) have their own Web site, and they are just as likely as other creators to have contributed to a family, business or organizational Web site. They have posted photos online (30%) as well as pieces of writing (27%). This group shies away from newer or more fraught content creating or sharing technologies. A little less than a third (31%) have downloaded music (similar to the number of Omnivores who sought religious information online), and only 4% have ever posted audio or video files, and only 6% have ever shared any artwork. As mentioned before only 13% have ever used a Webcam, and only 3% (compared to 12% of power users) have a blog.[2]
The collective community of all blogs and blog authors, particularly notable and widely read blogs, is known as the blogosphere. Since all blogs are on the internet by definition, they may be seen as interconnected and socially networked, through blogrolls, comments, linkbacks (refbacks, trackbacks or pingbacks), and backlinks. Discussions "in the blogosphere" were occasionally used by the media as a gauge of public opinion on various issues. Because new, untapped communities of bloggers and their readers can emerge in the space of a few years, Internet marketers pay close attention to "trends in the blogosphere
- 2008: As of 2008, blogging had become such a mania that a new blog was created every second of every minute of every hour of every day. Researchers have actively analyzed the dynamics of how blogs become popular. There are essentially two measures of this: popularity through citations, as well as popularity through affiliation (i.e., blogroll). The basic conclusion from studies of the structure of blogs is that while it takes time for a blog to become popular through blogrolls, permalinks can boost popularity more quickly, and are perhaps more indicative of popularity and authority than blogrolls, since they denote that people are actually reading the blog's content and deem it valuable or noteworthy in specific cases.
With the ubiquity and familiarity of the blog format, this term is now fairly redundant and almost never used.
Etymology
editThe same dictionary, by the way, defines blogosphere as "a word created with the [sole] purpose to be the worst sounding thing ever, second only to the originating term blog."
Back in the dawn of blogging — I started in September 2001 — a fellow blogospherian, Tony Pierce, turned his online diary into a book. I made the mistake of suggesting it should be called a "blook."
Jeff Jarvis is the director of the interactive journalism program at the City University of New York's Graduate School of Journalism. He is the author of What Would Google Do?
Ralph Orlowski/Getty Images
I'm sorry, OK? I'm very sorry. Please don't include that in my obit. Don't etch "blook" on my tombstone
Graham also said he'd rather be remembered for another neologism: "pentropy," defined as the contraction of the universe that causes ballpoints to disappear from your desk. Pentropy: It's all yours, sir.
I'm also accused by some of coining "Googlejuice," but I swear that's not my fault. I'm searching on Google now for someone else to blame.
To settle their dispute, Bill Quick and Brad Graham held a cordial discussion in blog comments in 2002. Quick conceded provenance of "blogosphere" to Graham. But Graham gave Quick credit for popularizing it. Besides, Graham said he preferred "blogmos" anyway.
In the mid-1990s, a handful of blog-like sites began appearing, like Justin's Links,
Originally meant to sound ridiculous, the terms "blog" and "blogosphere" were first used to satirize, but eventually replaced, the jargon used to describe an online genre and culture emerging in the late 1990s.
In the mid-1990s, a handful of blog-like sites began appearing, like Justin's Links,
the first personal web journals began appearing, quickly becoming a popular new genre that lacked a standardized, convenient name. Before summer the next year, Peter Merholz unintentional gave the genre its now standard name, explaining in a sidebar post that "decided to pronounce the word "weblog" as wee'- blog. Or "blog" for short." .[3]
jokingly started referring to the genre as a blog,
were first used as satire, original designed to sound ridiculous.
coined as satire. first used to satirize the language emerging for online personal journaling.
coined to satboth appear in posts about ridiculous language used to describe online personal journaling. a few months after the word Peter Merholz jokingly introduced the term blog. in a 1999 personal website post satirizing the popularity of the word . by Brad L. Graham. Bemoaning blog, lists "blogosphere" as one of . In a post his personal website The Bradlands, Graham First documented use of the term originally was used as a joke by on September 10, 1999 by Brad L. Graham, as a joke.[4][5] It was re-coined in 2002 by William Quick[6] and was quickly adopted and propagated by the warblog community. The term resembles the older word logosphere (from Greek logos meaning word, and sphere, interpreted as world), "the world of words", the universe of discourse.[7][8]
Despite the term's humorous intent, CNN, the BBC, and National Public Radio's programs Morning Edition, Day To Day, and All Things Considered have used it several times to discuss public opinion. A number of media outlets in recent years have started treating the blogosphere as a gauge of public opinion, and it has been cited in both academic and non-academic work as evidence of rising or falling resistance to globalization, voter fatigue, and many other phenomena,[9] and also in reference to identifying influential bloggers[10] and "familiar strangers" in the blogosphere.[11][12]
https://expbook.wordpress.com/2012/02/26/disappearance-of-blogs/
https://link.springer.com/referenceworkentry/10.1007/978-1-4614-6170-8_378
Blogosphere (alternate: blogsphere) is the collective term encompassing all weblogs or blogs; blogs as a community; blogs as a social network. Weblogs are densely interconnected; bloggers read others' blogs, link to them, reference them in their own writing, and post comments on each others' blogs. Because of this, the interconnected blogs have grown their own culture.
Blogosphere is an essential concept for blogs. Blogs themselves are just web formats, whereas the blogosphere is a social phenomenon. What really differentiates blogs from webpages or forums or chatrooms is that blogs are designed from the outset to be part of that shifting Internet-wide social network.
Through links and commentaries, the blogosphere with its self-perfecting mechanism, converts itself from a personal publishing system into a collaborative publishing system.
Sites such as Technorati [1], Blogdex [2], Blogrunner [3], Blog Street [4] and Truth Laid Bear [5] use the links made by bloggers to track the interconnections between bloggers. Taking advantage of hypertext links which act as markers for the subjects the bloggers are discussing, these sites can follow a piece of conversation as it moves from blog to blog. These also can help information researchers like MIT Media Lab study new communication technologies.
Proliferation
editIn 1999, Pyra Labs opened blogging to the masses by simplifying the process of creating and maintaining personal web spaces. Prior to the creation of Pyra's "Blogger", the number of blogs in existence was thought to be less than one hundred. Blogger led to the birth of the wider blogosphere.[13][14] In 2005, a Gallup poll showed that a third of Internet users read blogs at least on occasion,[15] and in May 2006, a study showed that there were over forty-two million bloggers contributing to the blogosphere. With less than 1 million blogs in existence at the start of 2003, the number of blogs had doubled in size every six months through 2006.[14]
In 2011, it was estimated that there were more than 158 million blogs, with more than 1 million new posts being produced by the blogosphere each day.[citation needed]
Revenue
editIn a 2010 Technorati study, 36% of bloggers reported some sort of income from their blogs, most often in the form of ad revenue.[16] This shows a steady increase from their 2009 report, in which 28% of the blogging world reported their blog as a source of income, with the mean annual income from advertisements at $42,548.[17] Other common sources of blog-related income are paid speaking engagements and paid postings.[16] Paid postings may be subject to rules on clearly disclosing commercial advertisements as such (regulated by, for example, the Federal Trade Commission in the US and the Advertising Standards Authority in the UK).
As a social network
editOnce popular sites, such as Technorati, BlogPulse, and Tailrank, now all defunct, sprung in the early 2000s to track the interconnections between bloggers. Taking advantage of hypertext links which act as markers for the subjects the bloggers are discussing, these sites followed conversations from blog to blog. Information researchers used such sites to study how quickly memes spread and the characteristics of influential websites.[18] Smaller blogosphere indexers also tracked specific blogospheres, such as those related by a certain genre, culture, subject matter, or geopolitical location.
Mapping
editIn 2007, following six weeks of observation, social media expert Matthew Hurst mapped the blogosphere, generating the plot to the left based on the interconnections between blogs. The most densely populated areas represent the most active portions of the blogosphere. White dots represent individual blogs. They are sized according to the number of links surrounding that particular blog. Links are plotted in both green and blue, with green representing one-way links and blue representing reciprocal links.[19]
DISCOVER Magazine described six major 'hot spots' of the blogosphere. While points 1 and 2 represent influential individual blogs, point 3 is the perfect example of "blogging island", where individual blogs are highly connected within a sub-community but lack many connections to the larger blogosphere. Point 4 describes a sociopolitical blogging niche, in which links demonstrate the constant dialogue between bloggers who write about the same subject of interest. Point 5 is an isolated sub-community of blogs dedicated to the world of pornography. Lastly, point 6 represents a collection of sports' lovers who largely segregate themselves but still manage to link back to the higher traffic blogs toward the center of the blogosphere.[19]
Merging with other social networks
editOver time, the blogosphere developed as its own network of interconnections. In this time, bloggers began to engage in other online communities, especially social networking sites, melding the two realms of social media together.
According to Technorati's 2010 "State of the Blogosphere" report, 78% of bloggers were using the microblogging service Twitter, with much larger percentages of individuals who blogged as a part-time job (88%) or full-time for a specific company (88%). Almost half of all bloggers surveyed used Twitter to interact with the readers of their blog, while 72% of bloggers used it for blog promotion. For bloggers whose blog was their business (self-employed), 63% used Twitter to market their business. Additionally, according to the report, almost 9 out of 10 (87%) bloggers were using Facebook.[16]
Blogging niches
editWithin the blogosphere, several sub-communities have developed. These communities are largely divided by genre. Blogs are often identified by a specific genre or topic, such as travel or politics.
- News blogs have become popular, and have created competition for traditional print newspaper and news magazines. The Huffington Post was ranked the most powerful blog in the world by The Observer in 2008,[20] and has come to dominate current event reporting.
- Political blogs are often tied to a large media or news corporation, such as "The Caucus" (affiliated with The New York Times), "CNN Political Ticker", and the National Review's "The Corner".
- Gossip blogs have grown extensively with the development of the blogosphere. One of the first influential gossip bloggers was Perez Hilton, a celebrity and entertainment media gossip blogger. His blog posts tabloid photographs of celebrities, accompanied by captions and comments. Web traffic to the often controversial and raunchy Perez Hilton site increased significantly in 2005, prompting similar gossip blogs, such as TMZ.com to gain popularity.[21]
- Food blogs allow chefs to share recipes, cooking techniques, and food porn. Food blogs such as 101 Cookbooks, Smitten Kitchen, and Simply Recipes can serve as online cookbooks for followers and often contain restaurant critiques, product reviews, and step-by-step photography for recipes.
- Fashion blogs have also become large sub-communities following the growth of the blogosphere. blogs like Racked, The Cut, and Fashionista give readers an eye into the fashion industry. Besides fashion news blogs, street style blogs have also become popular. Such bloggers include Scott Schuman (The Sartorialist), Tommy Ton (Jak and Jil), Jane Aldridge (Sea of Shoes), Bryan Grey-Yambao (Bryanboy), and Tavi Gevinson (Style Rookie). They are able to earn considerable livings through advertising, selling their photos and even providing their services as photographers, stylists, and guest designers.
- Health blogs cover health topics, events and/or related content of the health industry and the general community. A health blog can cover diverse health related concerns such as nutrition and diet, fitness, weight control, diseases, disease management, societal trends affecting health, analysis about health, business of health and health research.
- Scientific blogs cover different scientific and mathematical topics. Some of these are written by leading researchers, others by interested laymen. These are often free to access and thus provide an alternative to pay walled scientific literature.
- Genealogy blogs cover a variety of topics related to genealogy and family history, including the genealogy industry, genealogy software and technology, as well as educational "how to" posts related to specific research areas.
- Philosophy blogs both in analytic philosophy and Continental philosophy are a significant part of the blogosphere, often covering metaphysics, ethics and philosophy of language.
See also
editReferences
edit- ^ Fair, Ted; Nordfelt, Michael; Ring, Sandra; Cole, Eric (2005-01-01), Fair, Ted; Nordfelt, Michael; Ring, Sandra; Cole, Eric (eds.), "Chapter 10 - Advanced Techniques", Cyber Spying, Burlington: Syngress, pp. 343–376, ISBN 978-1-931836-41-8, retrieved 2022-02-10
- ^ Am; Lenhart, a; Fallows, Deborah; Horrigan, John B. (2004-02-29). "Content Creation Online". Pew Research Center: Internet, Science & Tech. Retrieved 2022-02-10.
- ^ "The first blog". www.netprolive.com. Retrieved 2022-02-10.
- ^ "Must See http://". The BradLands. 1999-09-10. Archived from the original on 2011-08-08. Retrieved 2011-12-26.
- ^ Axelrod, Laura (January 4, 2010). "Brad L. Graham, coined the term 'blogosphere,' dies at 41". The Birmingham News. Retrieved September 28, 2011.
- ^ DailyPundit.com (via Internet Archive)
- ^ "Logos." PBS.org. https://www.pbs.org/faithandreason/theogloss/logos-body.html
- ^ "Sphere." English for Students. http://www.english-for-students.com/sphere.html
- ^ Blogosphere in Web Archive at the Wayback Machine (archived July 13, 2011)Blogosphere: The new political arena, Michael Keren, 2006.
- ^ Nitin Agarwal, Huan Liu, Lei Tang, and Philip Yu. "Identifying Influential Bloggers in a Community", First International Conference on Web Search and Data Mining (WSDM08), February 11–12, Stanford, California.
- ^ Nitin Agarwal, Huan Liu, John Salerno, and Philip Yu. "Searching for 'Familiar Strangers' on Blogosphere: Problems and Challenges", NSF Symposium on Next-Generation Data Mining and Cyber-enabled Discovery and Innovation. October 10–12, Baltimore, MD.
- ^ Nitin Agarwal, Huan Liu, Sudheendra Murthy, Arunabha Sen, and Xufei Wang. "A Social Identity Approach to Identify Familiar Strangers in a Social Network", 3rd Int'l AAAI Conference on Weblogs and Social Media, May 17–20, 2009, San Jose, California.
- ^ "All About The Blogosphere". Into The Blogosphere.
- ^ a b Joust, K. & Hipolit, M. (2006). Blog explosion. CQ Researcher, 16(22), 505-528.
- ^ Saad, L. (2006). Blog Readership Bogged Down. Gallup. http://www.gallup.com/poll/21397/blog-readership-bogged-down.aspx.
- ^ a b c Sobel, J. (2010). State of the blogosphere.Retrieved October 3, 2011, from http://technorati.com/blogging/article/state-of-the-blogosphere-2010-introduction/ On web archive at the Wayback Machine (archived January 6, 2012)
- ^ Sussman, M. (2009). State of the blogosphere.Retrieved October 3, 2011, from"Archive link". Archived from the original on 2012-01-01. Retrieved 2011-10-04.
{{cite web}}: CS1 maint: bot: original URL status unknown (link) "Archived copy". Archived from the original on 2011-10-27. Retrieved 2011-10-04.{{cite web}}: CS1 maint: archived copy as title (link) - ^ Investigating the Impact of the Blogosphere: Using PageRank to Determine the Distribution of Attention Archived November 27, 2007, at the Wayback Machine, Kirchhoff, Bruns & Nicolai, 2007.
- ^ a b Ornes, S. (2007). Welcome to the blogosphere. DISCOVER Magazine. Retrieved October 3, 2011, from http://discovermagazine.com/2007/may/map-welcome-to-the-blogosphere
- ^ Aldred, Jessica (2008-03-09). "The world's 50 most powerful blogs". London: Observer. Retrieved 2008-09-23.
- ^ The designation itself is mentioned in, among others, Gray, Tyler (2006-09-28). "Pop goes Perez: How a pudgy Miami poseur became gossip's new queen". Radar Online. Retrieved 2007-02-1





