In analytical mechanics , a branch of applied mathematics and physics , a virtual displacement (or infinitesimal variation )
δ
γ
{\displaystyle \delta \gamma }
hypothetically (hence the term virtual ) deviate very slightly from the actual trajectory
γ
{\displaystyle \gamma }
[ 1] [ 2] [ 3] : 263
t
,
{\displaystyle t,}
δ
γ
(
t
)
{\displaystyle \delta \gamma (t)}
tangential to the configuration space at the point
γ
(
t
)
.
{\displaystyle \gamma (t).}
δ
γ
(
t
)
{\displaystyle \delta \gamma (t)}
γ
(
t
)
{\displaystyle \gamma (t)}
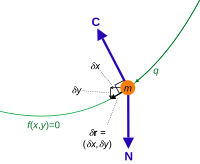
Constraint force C and virtual displacement δ r for a particle of mass m confined to a curve. The resultant non-constraint force is N . The components of virtual displacement are related by a constraint equation.
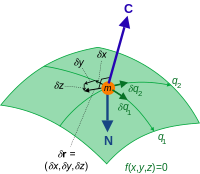
For example, the virtual displacements of the system consisting of a single particle on a two-dimensional surface fill up the entire tangent plane, assuming there are no additional constraints.
If, however, the constraints require that all the trajectories
γ
{\displaystyle \gamma }
q
{\displaystyle \mathbf {q} }
τ
,
{\displaystyle \tau ,}
γ
(
τ
)
=
q
,
{\displaystyle \gamma (\tau )=\mathbf {q} ,}
δ
γ
(
τ
)
=
0.
{\displaystyle \delta \gamma (\tau )=0.}
Let
M
{\displaystyle M}
configuration space of the mechanical system,
t
0
,
t
1
∈
R
{\displaystyle t_{0},t_{1}\in \mathbb {R} }
q
0
,
q
1
∈
M
,
{\displaystyle q_{0},q_{1}\in M,}
C
∞
[
t
0
,
t
1
]
{\displaystyle C^{\infty }[t_{0},t_{1}]}
smooth functions on
[
t
0
,
t
1
]
{\displaystyle [t_{0},t_{1}]}
P
(
M
)
=
{
γ
∈
C
∞
(
[
t
0
,
t
1
]
,
M
)
∣
γ
(
t
0
)
=
q
0
,
γ
(
t
1
)
=
q
1
}
.
{\displaystyle P(M)=\{\gamma \in C^{\infty }([t_{0},t_{1}],M)\mid \gamma (t_{0})=q_{0},\ \gamma (t_{1})=q_{1}\}.}
The constraints
γ
(
t
0
)
=
q
0
,
{\displaystyle \gamma (t_{0})=q_{0},}
γ
(
t
1
)
=
q
1
{\displaystyle \gamma (t_{1})=q_{1}}
For each path
γ
∈
P
(
M
)
{\displaystyle \gamma \in P(M)}
ϵ
0
>
0
,
{\displaystyle \epsilon _{0}>0,}
variation of
γ
{\displaystyle \gamma }
Γ
:
[
t
0
,
t
1
]
×
[
−
ϵ
0
,
ϵ
0
]
→
M
{\displaystyle \Gamma :[t_{0},t_{1}]\times [-\epsilon _{0},\epsilon _{0}]\to M}
ϵ
∈
[
−
ϵ
0
,
ϵ
0
]
,
{\displaystyle \epsilon \in [-\epsilon _{0},\epsilon _{0}],}
Γ
(
⋅
,
ϵ
)
∈
P
(
M
)
{\displaystyle \Gamma (\cdot ,\epsilon )\in P(M)}
Γ
(
t
,
0
)
=
γ
(
t
)
.
{\displaystyle \Gamma (t,0)=\gamma (t).}
virtual displacement
δ
γ
:
[
t
0
,
t
1
]
→
T
M
{\displaystyle \delta \gamma :[t_{0},t_{1}]\to TM}
(
T
M
{\displaystyle (TM}
tangent bundle of
M
)
{\displaystyle M)}
Γ
{\displaystyle \Gamma }
[ 1]
t
∈
[
t
0
,
t
1
]
{\displaystyle t\in [t_{0},t_{1}]}
tangent vector
δ
γ
(
t
)
=
d
Γ
(
t
,
ϵ
)
d
ϵ
|
ϵ
=
0
∈
T
γ
(
t
)
M
.
{\displaystyle \delta \gamma (t)=\left.{\frac {d\Gamma (t,\epsilon )}{d\epsilon }}\right|_{\epsilon =0}\in T_{\gamma (t)}M.}
In terms of the tangent map ,
δ
γ
(
t
)
=
Γ
∗
t
(
d
d
ϵ
|
ϵ
=
0
)
.
{\displaystyle \delta \gamma (t)=\Gamma _{*}^{t}\left(\left.{\frac {d}{d\epsilon }}\right|_{\epsilon =0}\right).}
Here
Γ
∗
t
:
T
0
[
−
ϵ
,
ϵ
]
→
T
Γ
(
t
,
0
)
M
=
T
γ
(
t
)
M
{\displaystyle \Gamma _{*}^{t}:T_{0}[-\epsilon ,\epsilon ]\to T_{\Gamma (t,0)}M=T_{\gamma (t)}M}
Γ
t
:
[
−
ϵ
,
ϵ
]
→
M
,
{\displaystyle \Gamma ^{t}:[-\epsilon ,\epsilon ]\to M,}
Γ
t
(
ϵ
)
=
Γ
(
t
,
ϵ
)
,
{\displaystyle \Gamma ^{t}(\epsilon )=\Gamma (t,\epsilon ),}
d
d
ϵ
|
ϵ
=
0
∈
T
0
[
−
ϵ
,
ϵ
]
.
{\displaystyle \textstyle {\frac {d}{d\epsilon }}{\Bigl |}_{\epsilon =0}\in T_{0}[-\epsilon ,\epsilon ].}
Coordinate representation. If
{
q
i
}
i
=
1
n
{\displaystyle \{q_{i}\}_{i=1}^{n}}
M
{\displaystyle M}
n
=
dim
M
,
{\displaystyle n=\dim M,}
δ
γ
(
t
)
=
∑
i
=
1
n
d
[
q
i
(
Γ
(
t
,
ϵ
)
)
]
d
ϵ
|
ϵ
=
0
⋅
d
d
q
i
|
γ
(
t
)
.
{\displaystyle \delta \gamma (t)=\sum _{i=1}^{n}{\frac {d[q_{i}(\Gamma (t,\epsilon ))]}{d\epsilon }}{\Biggl |}_{\epsilon =0}\cdot {\frac {d}{dq_{i}}}{\Biggl |}_{\gamma (t)}.}
If, for some time instant
τ
{\displaystyle \tau }
γ
∈
P
(
M
)
,
{\displaystyle \gamma \in P(M),}
γ
(
τ
)
=
const
,
{\displaystyle \gamma (\tau )={\text{const}},}
γ
∈
P
(
M
)
,
{\displaystyle \gamma \in P(M),}
δ
γ
(
τ
)
=
0.
{\displaystyle \delta \gamma (\tau )=0.}
If
γ
,
d
γ
d
t
∈
P
(
M
)
,
{\displaystyle \textstyle \gamma ,{\frac {d\gamma }{dt}}\in P(M),}
δ
d
γ
d
t
=
d
d
t
δ
γ
.
{\displaystyle \delta {\frac {d\gamma }{dt}}={\frac {d}{dt}}\delta \gamma .}
A single particle freely moving in
R
3
{\displaystyle \mathbb {R} ^{3}}
M
=
R
3
,
{\displaystyle M=\mathbb {R} ^{3},}
P
(
M
)
=
C
∞
(
[
t
0
,
t
1
]
,
M
)
.
{\displaystyle P(M)=C^{\infty }([t_{0},t_{1}],M).}
γ
∈
P
(
M
)
{\displaystyle \gamma \in P(M)}
Γ
(
t
,
ϵ
)
{\displaystyle \Gamma (t,\epsilon )}
γ
,
{\displaystyle \gamma ,}
σ
∈
T
0
R
3
{\displaystyle \sigma \in T_{0}\mathbb {R} ^{3}}
Γ
(
t
,
ϵ
)
=
γ
(
t
)
+
σ
(
t
)
ϵ
+
o
(
ϵ
)
,
{\displaystyle \Gamma (t,\epsilon )=\gamma (t)+\sigma (t)\epsilon +o(\epsilon ),}
ϵ
→
0.
{\displaystyle \epsilon \to 0.}
δ
γ
(
t
)
=
(
d
d
ϵ
(
γ
(
t
)
+
σ
(
t
)
ϵ
+
o
(
ϵ
)
)
)
|
ϵ
=
0
{\displaystyle \delta \gamma (t)=\left.\left({\frac {d}{d\epsilon }}{\Bigl (}\gamma (t)+\sigma (t)\epsilon +o(\epsilon ){\Bigr )}\right)\right|_{\epsilon =0}}
which leads to
δ
γ
(
t
)
=
σ
(
t
)
∈
T
γ
(
t
)
R
3
.
{\displaystyle \delta \gamma (t)=\sigma (t)\in T_{\gamma (t)}\mathbb {R} ^{3}.}
Free particles on a surface
edit
N
{\displaystyle N}
S
⊂
R
3
{\displaystyle S\subset \mathbb {R} ^{3}}
2
N
{\displaystyle 2N}
M
=
{
(
r
1
,
…
,
r
N
)
∈
R
3
N
∣
r
i
∈
R
3
;
r
i
≠
r
j
if
i
≠
j
}
,
{\displaystyle M=\{(\mathbf {r} _{1},\ldots ,\mathbf {r} _{N})\in \mathbb {R} ^{3\,N}\mid \mathbf {r} _{i}\in \mathbb {R} ^{3};\ \mathbf {r} _{i}\neq \mathbf {r} _{j}\ {\text{if}}\ i\neq j\},}
where
r
i
∈
R
3
{\displaystyle \mathbf {r} _{i}\in \mathbb {R} ^{3}}
i
th
{\displaystyle i^{\text{th}}}
T
(
r
1
,
…
,
r
N
)
M
=
T
r
1
S
⊕
…
⊕
T
r
N
S
,
{\displaystyle T_{(\mathbf {r} _{1},\ldots ,\mathbf {r} _{N})}M=T_{\mathbf {r} _{1}}S\oplus \ldots \oplus T_{\mathbf {r} _{N}}S,}
and every path
γ
∈
P
(
M
)
{\displaystyle \gamma \in P(M)}
r
i
{\displaystyle \mathbf {r} _{i}}
γ
(
t
)
=
(
r
1
(
t
)
,
…
,
r
N
(
t
)
)
.
{\displaystyle \gamma (t)=(\mathbf {r} _{1}(t),\ldots ,\mathbf {r} _{N}(t)).}
This implies that, for every
δ
γ
(
t
)
∈
T
(
r
1
(
t
)
,
…
,
r
N
(
t
)
)
M
,
{\displaystyle \delta \gamma (t)\in T_{(\mathbf {r} _{1}(t),\ldots ,\mathbf {r} _{N}(t))}M,}
δ
γ
(
t
)
=
δ
r
1
(
t
)
⊕
…
⊕
δ
r
N
(
t
)
,
{\displaystyle \delta \gamma (t)=\delta \mathbf {r} _{1}(t)\oplus \ldots \oplus \delta \mathbf {r} _{N}(t),}
where
δ
r
i
(
t
)
∈
T
r
i
(
t
)
S
.
{\displaystyle \delta \mathbf {r} _{i}(t)\in T_{\mathbf {r} _{i}(t)}S.}
δ
γ
=
(
δ
r
1
,
…
,
δ
r
N
)
.
{\displaystyle \delta \gamma =(\delta \mathbf {r} _{1},\ldots ,\delta \mathbf {r} _{N}).}
Rigid body rotating around fixed point
edit
A rigid body rotating around a fixed point with no additional constraints has 3 degrees of freedom. The configuration space here is
M
=
S
O
(
3
)
,
{\displaystyle M=SO(3),}
special orthogonal group of dimension 3 (otherwise known as 3D rotation group ), and
P
(
M
)
=
C
∞
(
[
t
0
,
t
1
]
,
M
)
.
{\displaystyle P(M)=C^{\infty }([t_{0},t_{1}],M).}
s
o
(
3
)
{\displaystyle {\mathfrak {so}}(3)}
skew-symmetric three-dimensional matrices. The exponential map
exp
:
s
o
(
3
)
→
S
O
(
3
)
{\displaystyle \exp :{\mathfrak {so}}(3)\to SO(3)}
ϵ
0
>
0
{\displaystyle \epsilon _{0}>0}
γ
∈
P
(
M
)
,
{\displaystyle \gamma \in P(M),}
Γ
(
t
,
ϵ
)
,
{\displaystyle \Gamma (t,\epsilon ),}
t
∈
[
t
0
,
t
1
]
,
{\displaystyle t\in [t_{0},t_{1}],}
Θ
t
∈
C
∞
(
[
−
ϵ
0
,
ϵ
0
]
,
s
o
(
3
)
)
{\displaystyle \Theta ^{t}\in C^{\infty }([-\epsilon _{0},\epsilon _{0}],{\mathfrak {so}}(3))}
Θ
t
(
0
)
=
0
{\displaystyle \Theta ^{t}(0)=0}
ϵ
∈
[
−
ϵ
0
,
ϵ
0
]
,
{\displaystyle \epsilon \in [-\epsilon _{0},\epsilon _{0}],}
Γ
(
t
,
ϵ
)
=
γ
(
t
)
exp
(
Θ
t
(
ϵ
)
)
.
{\displaystyle \Gamma (t,\epsilon )=\gamma (t)\exp(\Theta ^{t}(\epsilon )).}
δ
γ
(
t
)
=
(
d
d
ϵ
(
γ
(
t
)
exp
(
Θ
t
(
ϵ
)
)
)
)
|
ϵ
=
0
=
γ
(
t
)
d
Θ
t
(
ϵ
)
d
ϵ
|
ϵ
=
0
.
{\displaystyle \delta \gamma (t)=\left.\left({\frac {d}{d\epsilon }}{\Bigl (}\gamma (t)\exp(\Theta ^{t}(\epsilon )){\Bigr )}\right)\right|_{\epsilon =0}=\gamma (t)\left.{\frac {d\Theta ^{t}(\epsilon )}{d\epsilon }}\right|_{\epsilon =0}.}
Since, for some function
σ
:
[
t
0
,
t
1
]
→
s
o
(
3
)
,
{\displaystyle \sigma :[t_{0},t_{1}]\to {\mathfrak {so}}(3),}
Θ
t
(
ϵ
)
=
ϵ
σ
(
t
)
+
o
(
ϵ
)
{\displaystyle \Theta ^{t}(\epsilon )=\epsilon \sigma (t)+o(\epsilon )}
ϵ
→
0
{\displaystyle \epsilon \to 0}
δ
γ
(
t
)
=
γ
(
t
)
σ
(
t
)
∈
T
γ
(
t
)
S
O
(
3
)
.
{\displaystyle \delta \gamma (t)=\gamma (t)\sigma (t)\in T_{\gamma (t)}\mathrm {SO} (3).}