Under construction. The infobox is not yet revised. The article is not yet revised. The references have not been revised.
|
Probability density function 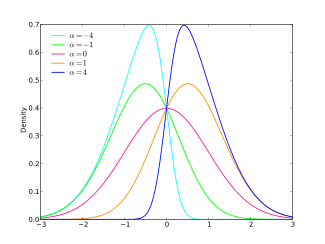 | |||
|
Cumulative distribution function 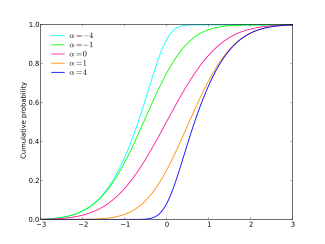 | |||
| Parameters |
location (real) scale (positive, real) shape (real) | ||
|---|---|---|---|
| Support | |||
| CDF |
isOwen's T function | ||
| Mean | where | ||
| Variance | |||
| Skewness | |||
| Excess kurtosis | |||
| MGF | |||
In probability theory and statistics, the skew elliptical distribution is a continuous probability distribution that generalizes the family of elliptically symmetric distributions to allow for non-zero skewness.
Definition
editLet denote the standard normal probability density function
with the cumulative distribution function given by
where erf is the error function. Then the probability density function of the skew-normal distribution with parameter α is given by
This distribution was first introduced by O'Hagan and Leonhard (1976).
To add location and scale parameters to this, one makes the usual transform . One can verify that the normal distribution is recovered when , and that the absolute value of the skewness increases as the absolute value of increases. The distribution is right skewed if and is left skewed if . The probability density function with location , scale , and parameter becomes
Note, however, that the skewness of the distribution is limited to the interval .
Estimation
editMaximum likelihood estimates for , , and can be computed numerically, but no closed-form expression for the estimates is available unless . If a closed-form expression is needed, themethod of moments can be applied to estimate from the sample skew, by inverting the skewness equation. This yields the estimate
where , and is the sample skew. The sign of is the same as the sign of . Consequently, .
The maximum (theoretical) skewness is obtained by setting in the skewness equation, giving . However it is possible that the sample skewness is larger, and then cannot be determined from these equations. When using the method of moments in an automatic fashion, for example to give starting values for maximum likelihood iteration, one should therefore let (for example) .
See also
editReferences
edit- Azzalini, A. (1985). "A class of distributions which includes the normal ones". Scand. J. Statist. 12: 171–178.
{{cite journal}}: Cite has empty unknown parameter:|coauthors=(help)
- O'Hagan, A. and Leonhard, T. (1976). Bayes estimation subject to uncertainty about parameter constraints. Biometrika, 63, 201-202.












